题目内容
13.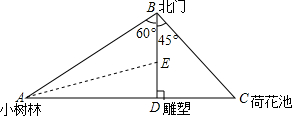 某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:
某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:(1)分别求线段AB、BC、AC的长(结果中保留根号,下同);
(2)若有一颗银杏树E恰好位于∠BAD的平分线与BD的交点,求BE的距离.
分析 (1)先解Rt△ABD,根据锐角三角函数的定义得出AB=$\frac{BD}{cos60°}$=200米,AD=BD•tan60°=100$\sqrt{3}$米.再解Rt△CBD中,得出DC=BD=100米,BC=$\sqrt{2}$BD=100$\sqrt{2}$米,那么AC=AD+DC=(100$\sqrt{3}$+100)米;
(2)作EF⊥AB于F,根据角平分线性质得出EF=ED.利用HL证明△AEF≌△AED,得出AF=AD=100$\sqrt{3}$米,于是BF=AB-AF=(200-100$\sqrt{3}$)米.然后在Rt△BEF中,根据30°角所对的直角边等于斜边的一半得出BE=2BF=(400-200$\sqrt{3}$)米.
解答 解:(1)∵在Rt△ABD中,∠ADB=90°,∠ABD=60°,BD=100米,
∴AB=$\frac{BD}{cos60°}$=200米,AD=BD•tan60°=100$\sqrt{3}$米.
∵在Rt△CBD中,∠CDB=90°,∠CBD=45°,BD=100米,
∴DC=BD=100米,BC=$\sqrt{2}$BD=100$\sqrt{2}$米,
∴AC=AD+DC=(100$\sqrt{3}$+100)米; (2)作EF⊥AB于F,
(2)作EF⊥AB于F,
∵AE平分∠BAD,ED⊥AD于D,EF⊥AB于F,
∴EF=ED.
在Rt△AEF与Rt△AED中,
$\left\{\begin{array}{l}{AE=AE}\\{EF=ED}\end{array}\right.$,
∴△AEF≌△AED(HL),
∴AF=AD=100$\sqrt{3}$米,
∴BF=AB-AF=(200-100$\sqrt{3}$)米.
∵在Rt△BEF中,∠EFB=90°,∠BEF=90°-60°=30°,
∴BE=2BF=(400-200$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,角平分线性质,全等三角形的判定与性质,准确作出辅助线是解题的关键.

| A. | tan30° | B. | $\root{3}{8}$ | C. | $\frac{1}{3}$ | D. | $\sqrt{49}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{15}{36}$ | C. | $\frac{4}{11}$ | D. | $\frac{5}{9}$ |
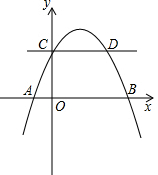 如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D.
如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D. 如图,在Rt△ABC中,∠C=90°,AC=BC,点D在AB的垂直平分线上,∠DAB=15°且AD=10cm,求BC的长.
如图,在Rt△ABC中,∠C=90°,AC=BC,点D在AB的垂直平分线上,∠DAB=15°且AD=10cm,求BC的长.