题目内容
10．
如图，若DE是△ABC的中位线，则S△ADE：S△ABC=（ ）| A． | 1：$\sqrt{2}$ | B． | 1：2 | C． | 1：3 | D． | 1：4 |
分析 由DE为三角形ABC的中位线，根据三角形中位线定理得到DE平行于BC，且DE等于BC的一半，可得出三角形ADE与三角形ABC相似，且相似比为1：2，根据相似三角形的面积之比等于相似比的平方，即可得到三角形ADE与三角形ABC面积之比．
解答 解：∵DE是△ABC的中位线，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴∠ADE=∠B，∠AED=∠C，
∴△ADE∽△ABC，且相似比为1：2，
∴S△ADE：S△ABC=1：4，
故选D．
点评 此题考查了相似三角形的判定与性质，三角形的中位线定理，以及平行线的性质，熟练掌握相似三角形的判定与性质是解本题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
1．下列说法正确的是（ ）
| A． | 掷一枚质地均匀的骰子，“向上一面的点数是6”是必然事件 | |
| B． | 了解一批电视机的使用寿命，适合用普查的方式 | |
| C． | “明天降雨的概率为$\frac{1}{2}$”，表示明天有半天都在降雨 | |
| D． | 在统计中，样本的方差可以近似地反映总体的波动大小 |
抛物线y=ax2-2ax-3a与x轴交于A、B两点（其中A在左侧，B在右侧，且经过点C（2，3）．
2．为执行“两免一补”政策，某地区2015年投入教育经费2700万元，预计2016年、2017年两年共投入6775万元，设这两年投入教育经费的年平均增长百分率为x，那么下面列出的方程正确的是（ ）
| A． | 2700x2=6775 | B． | 2700（1+x%）2=6775 | ||
| C． | 2700（1+x）2=6775 | D． | 2700（1+x）+2700（1+x）2=6775 |
已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：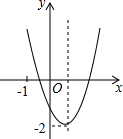
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根，下列结论：