题目内容
20. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:
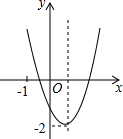
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2,
其中,正确的个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 直接利用抛物线与x轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间关系分析得出答案.
解答 解:如图所示:图象与x轴有两个交点,则b2-4ac>0,故①错误;
∵图象开口向上,∴a>0,
∵对称轴在y轴右侧,
∴a,b异号,
∴b<0,
∵图象与y轴交于x轴下方,
∴c<0,
∴abc>0,故②正确;
当x=-1时,a-b+c>0,故此选项错误;
∵二次函数y=ax2+bx+c的顶点坐标纵坐标为:-2,
故二次函数y=ax2+bx+c向上平移小于2个单位,则平移后解析式y=ax2+bx+c-m与x轴有两个交点,此时关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,
故-m<2,
解得:m>-2,
故④正确.
故选:B.
点评 此题主要考查了二次函数图象与系数的关系,正确把握二次函数与方程之间的关系是解题关键.

练习册系列答案
相关题目
10. 如图,若DE是△ABC的中位线,则S△ADE:S△ABC=( )
如图,若DE是△ABC的中位线,则S△ADE:S△ABC=( )
 如图,若DE是△ABC的中位线,则S△ADE:S△ABC=( )
如图,若DE是△ABC的中位线,则S△ADE:S△ABC=( )| A. | 1:$\sqrt{2}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
5.-2的相反数是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -$\frac{1}{2}$ |
 如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=$\sqrt{3}$-1.
如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=$\sqrt{3}$-1.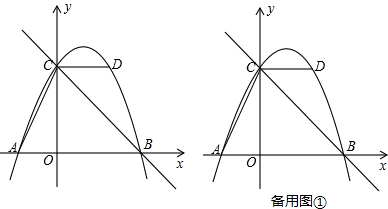
 如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2)、B($\frac{1}{2}$,n).
如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2)、B($\frac{1}{2}$,n).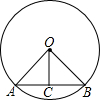 如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$.
如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$.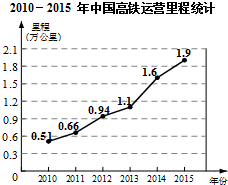 我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.
我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.