题目内容
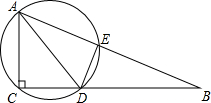 如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.(1)求证:AC=AE;
(2)求线段DE的长;
(3)求△ABC的外接圆的面积.
考点:三角形的外接圆与外心,全等三角形的判定与性质,勾股定理
专题:
分析:(1)由圆O的圆周角∠ACB=90°,根据90°的圆周角所对的弦为圆的直径得到AD为圆O的直径,再根据直径所对的圆周角为直角可得三角形ADE为直角三角形,又AD是△ABC的角平分线,可得一对角相等,而这对角都为圆O的圆周角,根据同圆或等圆中,相等的圆周角所对的弦相等可得CD=ED,利用HL可证明直角三角形ACD与AED全等,根据全等三角形的对应边相等即可得证;
(2)先根据勾股定理求出AB的长,再利用AE=AC,CD=DE结合勾股定理得出DE的长;
(3)根据直角三角形斜边的中点即是其外接圆的圆心,即可得出外接圆半径长,进而得出结论.
(2)先根据勾股定理求出AB的长,再利用AE=AC,CD=DE结合勾股定理得出DE的长;
(3)根据直角三角形斜边的中点即是其外接圆的圆心,即可得出外接圆半径长,进而得出结论.
解答: (1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又∵AD是△ABC的∠BAC的平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,
∴AB=
=
=13,
设DE=x,则BD=12-x,BE=13-5=8,
故x2+82=(12-x)2,
解得:x=
,
故DE的长为:
;
(3)解:由(2)得:△ABC外接圆的半径=
AB=
×13=
,
故△ABC的外接圆的面积为:π×(
)2=
π.
 (1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又∵AD是△ABC的∠BAC的平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,
∴AB=
| AC2+CB2 |
| 52+122 |
设DE=x,则BD=12-x,BE=13-5=8,
故x2+82=(12-x)2,
解得:x=
| 10 |
| 3 |
故DE的长为:
| 10 |
| 3 |
(3)解:由(2)得:△ABC外接圆的半径=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
故△ABC的外接圆的面积为:π×(
| 13 |
| 2 |
| 169 |
| 4 |
点评:本题考查的是圆周角定理,涉及到勾股定理,全等三角形的判定与性质等知识,能灵活运用圆周角定理及勾股定理是解本题的关键.

练习册系列答案
相关题目
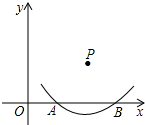 如上图,在直角坐标系中,以点P为圆心2
如上图,在直角坐标系中,以点P为圆心2| 5 |
A、(4,
| ||
| B、(4,2) | ||
| C、(4,4) | ||
D、(2,2
|
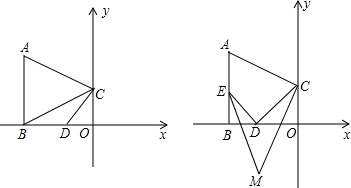
 如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.