题目内容
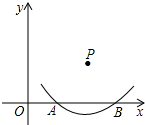 如上图,在直角坐标系中,以点P为圆心2
如上图,在直角坐标系中,以点P为圆心2| 5 |
A、(4,
| ||
| B、(4,2) | ||
| C、(4,4) | ||
D、(2,2
|
考点:垂径定理,坐标与图形性质,勾股定理
专题:
分析:首先连接PA、PB.过点P作PD⊥AB于点,根据垂径定理可得AD=2,再利用勾股定理计算出PD长即可.
解答:解:连接PA、PB.过点P作PD⊥AB于点D ,
,
∵A(2,0),B(6,0),
∴AB=4,
∵PD⊥AB,
∴AD=2,
∴DP=
=4,
∴P(4,4),
故选:C.
 ,
,∵A(2,0),B(6,0),
∴AB=4,
∵PD⊥AB,
∴AD=2,
∴DP=
(2
|
∴P(4,4),
故选:C.
点评:此题主要考查了垂径定理,关键是掌握平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
 如图,那么下列结论正确的是( )
如图,那么下列结论正确的是( )| A、a比b大 |
| B、b比a大 |
| C、a、b一样大 |
| D、a、b的大小无法确定 |
一个数的绝对值等于4,这个数是( )
| A、4 | B、-4 | C、±4 | D、±8 |
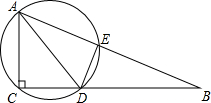 如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE. △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.