题目内容
20．已知△ABC中，∠A的余角是∠B的补角的$\frac{1}{4}$，且∠B大于100°，求∠A的取值范围．分析 设∠A的余角为90°-∠A，∠B的补角为180°-∠B，再根据三角形内角和列出不等式解答即可．
解答 解：∵∠A的余角是∠B的补角的$\frac{1}{4}$，
∴90°-∠A=$\frac{1}{4}$（180°-∠B），
∴可得：∠A=45°+$\frac{1}{4}$∠B，
可得：∠B=4∠A-180°，
可得4∠A-180°＞100°，
解得：∠A＞70°．
因为三角形内角和是180°，
所以可得∠A＜180°-100°=80°，
所以∠A的取值范围是70°＜∠A＜80°．
点评 此题考查余角的定义，关键是根据题意列出不等式．
练习册系列答案
相关题目
8．
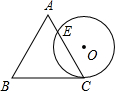如图，一个边长为a的等边三角形ABC的高与⊙O的直径相等，⊙O与BC相切于点C，⊙O与AC相交于点E，则AE：EC的值为（ ）
如图，一个边长为a的等边三角形ABC的高与⊙O的直径相等，⊙O与BC相切于点C，⊙O与AC相交于点E，则AE：EC的值为（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
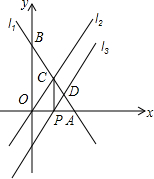如图，已知直线l1：y=-2x+8与两坐标轴分别相交于A、B两点，与直线l2：y=2x相交于点C，点P为x轴上的一个动点，过点P的直线，l3∥l2，且与l1相交于点D．