题目内容
18.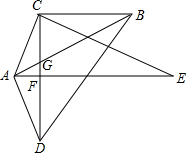 在Rt△ACE中,CF⊥AE于F,延长CF于D,使CF=FD,连结AD,G为CF上一点,连结AG并延长至B,连结BD和BC,使∠CBA=∠ABD=∠E.
在Rt△ACE中,CF⊥AE于F,延长CF于D,使CF=FD,连结AD,G为CF上一点,连结AG并延长至B,连结BD和BC,使∠CBA=∠ABD=∠E.(I)求证:△ACG∽△DBG:
(2)求证:AC2=AG•AB;
(3)若AC=$\sqrt{5}$,AE=5,且CG:CD=1:4.求AB和BD的长.
分析 (1)由∠CGA=∠BGD,根据余角的性质得到∠ACG=∠E,即可得到结论;
(2)通过△ACG∽△DBG,得到∠ACG=∠DBG,由∠ACG=∠CBA,推出△AGC∽ACB 根据相似三角形的性质即可得到结论;
(3)根据勾股定理得到CE=$\sqrt{A{E}^{2}-A{C}^{2}}$=2$\sqrt{5}$,由三角形的面积公式得到$\frac{1}{2}$•AC•CE=$\frac{1}{2}$•AE•CF,求得CF=2 CD=CF+FD=CF+CF=4 AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=1,得到CG=1,根据勾股定理AG=$\sqrt{G{F}^{2}+A{F}^{2}}$=$\sqrt{2}$,由于△ACG∽△DBG,得到比例式$\frac{AC}{DB}=\frac{AG}{DG}$,求得DB=$\frac{3\sqrt{10}}{2}$,如果根据比例式$\frac{CG}{BG}=\frac{AG}{DG}$,求得BG=$\frac{3\sqrt{2}}{2}$,即可得到结论.
解答 解:(1)∵∠CGA=∠BGD,
又∵∠ACG+∠ECG=∠ECG+∠E=90°,
∴∠ACG=∠E,
∴∠ACG=∠ABD,
∴△ACG∽△DBG;
(2)∵∠CAG=∠CAB,
又∵△ACG∽△DBG,
∴∠ACG=∠DBG,
即∠ACG=∠ABD,
∴∠ACG=∠CBA,
∴△AGC∽ACB
∴$\frac{AC}{AB}=\frac{AG}{AC}$,
∴AC2=AB•AG;
(3)∵CE=$\sqrt{A{E}^{2}-A{C}^{2}}$=2$\sqrt{5}$,
∴S△ACE=$\frac{1}{2}$•AC•CE=$\frac{1}{2}$•AE•CF,
∴CF=2 CD=CF+FD=CF+CF=4 AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=1,
∵$\frac{CG}{CD}$=$\frac{1}{4}$,
∴$\frac{CG}{4}$=$\frac{1}{4}$,
∴CG=1,
∴GF=CF-CG=2-1=1,
∴GD=CD-CG=4-1=3,
∴AG=$\sqrt{G{F}^{2}+A{F}^{2}}$=$\sqrt{2}$,又∵△ACG∽△DBG,
∴$\frac{AC}{DB}=\frac{AG}{DG}$,
∴$\frac{\sqrt{5}}{DB}=\frac{\sqrt{2}}{3}$,
∴DB=$\frac{3\sqrt{10}}{2}$,
∴$\frac{CG}{BG}=\frac{AG}{DG}$,
∴$\frac{1}{BG}=\frac{\sqrt{2}}{3}$,
∴BG=$\frac{3\sqrt{2}}{2}$,
∴AB=AG+BG,
∴AB=$\sqrt{2}$+$\frac{3\sqrt{2}}{2}$=$\frac{5\sqrt{2}}{2}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,三角形的面积,熟练掌握相似三角形的判定和性质是解题的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案一.以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二.个人所得税纳税税率如表所示:
| 纳税级数 | 个人每月应纳税所得额 | 税率 |
| 1 | 不超过1500元的部分 | 3% |
| 2 | 超过1500元至4500元的部分 | 10% |
| 3 | 超过4500元至9000元的部分 | 20% |
| 4 | 超过9000元至35000元的部分 | 25% |
| 5 | 超过35000元至55000元的部分 | 30% |
| 6 | 超过55000元至80000元的部分 | 35% |
| 7 | 超过80000元的部分 | 45% |
(2)若丙每月收入为x元,且8000<x<12500,写出丙每月缴纳的个人所得税y(元)与x的函数关系式.
| A. | 如果∠AOB=∠COD,那么$\widehat{AB}$=$\widehat{CD}$ | B. | 如果$\widehat{AB}$=$\widehat{CD}$,那么∠AOB=∠COD | ||
| C. | 如果$\widehat{AB}$=$\widehat{CD}$,那么AB=CD | D. | 如果AB=CD,那么$\widehat{AB}$=$\widehat{CD}$ |

 已知:如图,$\frac{AD}{AC}=\frac{DE}{AB}=\frac{AE}{BC}$,求证:AB=AE.
已知:如图,$\frac{AD}{AC}=\frac{DE}{AB}=\frac{AE}{BC}$,求证:AB=AE.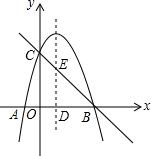 如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.
如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.