题目内容
如图，已知△ABC≌△ADE，试证明：∠1=∠B+∠C．考点：全等三角形的性质
专题：证明题
分析：根据已知全等三角形的性质得到：∠E=∠C，∠ADE=∠B．然后由三角形外角的性质证得结论．
解答：证明：∵△ABC≌△ADE，
∴∠E=∠C，∠ADE=∠B，
∴∠E+∠ADE=∠C+∠B．
又∵∠1=∠E+∠ADE，
∴∠1=∠B+∠C．
∴∠E=∠C，∠ADE=∠B，
∴∠E+∠ADE=∠C+∠B．
又∵∠1=∠E+∠ADE，
∴∠1=∠B+∠C．
点评：本题考查了全等三角形的性质．全等三角形的性质是证明线段和角相等的理论依据，应用时要会找对应角和对应边．
练习册系列答案
相关题目
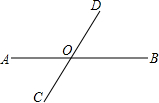如图，直线AB，CD相交于点O，∠AOD比∠BOD大60°，求∠AOD与∠BOD的大小．分式方程1-
=
的解为（ ）
| 2x |
| x-1 |
| 3 |
| x-1 |
| A、x=3 | B、x=-3 |
| C、x=4 | D、x=-4 |