题目内容
19.如图1,正六边形ABCDEF的面积为1,把它的各边延长一倍得到新正六边形$\frac{3}{2}$(如图2),称为第一次扩展;则正六边形$\frac{{\sqrt{2}}}{2}$的面积为3;把正六边形$\frac{{\sqrt{2}}}{2}$边长按原法延长一倍得到正六边形A2B2C2D2E2F2(如图3),称为第二次扩展;如此下去…,第n次扩展得到正六边形AnBnCnDnEnFn的面积为3n.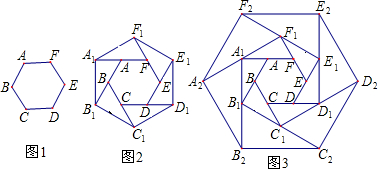
分析 本题建立在正六边形背景上,进行逐渐的图形“拓展”变化,进而从特殊到一般进行归纳总结拓展后正六边形面积与原正六边形面积之间的规律,复杂图形中含有基本图形(2),为学生研究提供的基本图形,进而得出从特殊归纳出一般性规律.
解答  解:∵拓展前后正六边形是彼此相似的,∴可以利用相似图形的性质求出相似比,从而求出拓展后六边形的面积,
解:∵拓展前后正六边形是彼此相似的,∴可以利用相似图形的性质求出相似比,从而求出拓展后六边形的面积,
∵正六边形ABCDEF的面积为1,把它的各边延长一倍得到新正六边形A1B1C1D1E1F1(如图2),
则EF=FF1,DE=EE1,
∴EE1=$\frac{1}{2}$F1E,∠EE1F1=90°,
∴$\frac{EF}{{E}_{1}{F}_{1}}$=$\frac{1}{\sqrt{3}}$,
∴正六边形A1B1C1D1E1F1面积为:3,
∴正六边形A2B2C2D2E2F2面积为:9,
以此类推得出,第n次扩展得到正六边形AnBnCnDnEnFn的面积为:3n.
故答案为:3,3n.
点评 此题主要考查了正多边形的性质与相似图形的性质,本题解决的关键是寻找到拓展的正六边形的面积于被拓展的正六边形面积之间的关系.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.对于任意正整数n,按下列程序计算下去,得到的结果是( )


| A. | 随n的变化而变化 | B. | 不变,总是0 | C. | 不变,定值为1 | D. | 不变,定值为2 |
14.已知点A(-3,y1),B(-1,y2),C(3,y3)都在反比例函数y=$\frac{4}{x}$的图象上,则( )
| A. | y3<y2<y1 | B. | y2>y1>y3 | C. | y1<y2<y3 | D. | y2<y1<y3 |
8.已知a-b=5,则a2-b2-10b+1的值为( )
| A. | 5 | B. | 6 | C. | 25 | D. | 26 |
9.以下关于一元二次方程的根的说法中,正确的是( )
| A. | 方程x2+x-2=0有一根为-1 | |
| B. | 方程x2+x=0有一根为1 | |
| C. | 方程x2+3x-4=0有两个不相等的实数根 | |
| D. | 方程x2+4=0有两个实数根,并且这两根互为相反数 |
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.请你画出以下图形:
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.请你画出以下图形: