题目内容
已知抛物线y=x2-(t+1)x+c(t,c是常数)与x轴的公共点的坐标为(m,0),(n,0),且0<m<n<1,则m与t的大小关系为 .
考点:抛物线与x轴的交点
专题:
分析:根据二次函数的对称性可得到m、n、t之间的关系式,再结合所给条件消去n,可找到m与t之间的关系,可判断其大小关系.
解答:解:
∵y=x2-(t+1)x+c,
∴其对称轴为x=
,
∵与x轴交于(m,0)、(n,0)两点,
∴
=
,
整理可得n=t+1-m,
又0<m<n<1,
∴n<1,
∴t+1-m<1,
即t<m,
故答案为:m>t.
∵y=x2-(t+1)x+c,
∴其对称轴为x=
| t+1 |
| 2 |
∵与x轴交于(m,0)、(n,0)两点,
∴
| m+n |
| 2 |
| t+1 |
| 2 |
整理可得n=t+1-m,
又0<m<n<1,
∴n<1,
∴t+1-m<1,
即t<m,
故答案为:m>t.
点评:本题主要考查二次函数的对称性质,掌握二次函数与x轴的两个交点关于对称轴对称是解题的关键.

练习册系列答案
相关题目
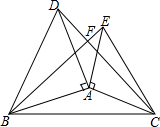 将等腰直角三角尺ABD、ACE如图放置,连接BE、CD.
将等腰直角三角尺ABD、ACE如图放置,连接BE、CD.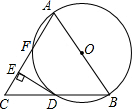 AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证:
AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证: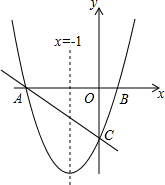 如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0). 如图所示,菱形ABCD的对角线AC=8cm,BD=6cm,AC与BD相交于点O,求tan
如图所示,菱形ABCD的对角线AC=8cm,BD=6cm,AC与BD相交于点O,求tan