题目内容
12.已知:2|a-1|+4(b-3)2=0.求:$\frac{1}{ab}+\frac{1}{(a+2)(b+2)}+\frac{1}{(a+4)(b+4)}+…+\frac{1}{(a+2018)(b+2018)}$.分析 根据非负数的性质可求出a=1,b=3,则原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2019×2021}$,然后进行分数的运算.
解答 解:∵2|a-1|+4(b-3)2=0,
∴a-1=0,b-3=0,解得a=1,b=3,
原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2019×2021}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2019}$-$\frac{1}{2021}$)
=$\frac{1}{2}$(1-$\frac{1}{2021}$)
=$\frac{1010}{2021}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了非负数的性质.

练习册系列答案
相关题目
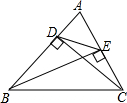 如图,CD,BE是△ABC的两条高,求证:△ABC∽△AED.
如图,CD,BE是△ABC的两条高,求证:△ABC∽△AED. 如图,BC的垂直平分线交AB于点D,若∠A=40°,且∠2=2∠1,求∠B,∠ACB.
如图,BC的垂直平分线交AB于点D,若∠A=40°,且∠2=2∠1,求∠B,∠ACB.