题目内容
2.用一根长为a的铁丝分别围成长和宽之比为2:1的长方形、正方形和圆三种图形,试分别用含a的代数式表示围成后这三个图形的面积,猜想并通过取数验证同样长的铁丝围成什么图形的面积会最大?分析 设长方形的宽为x,则长为2x,用a表示x得到x=$\frac{1}{6}$a,利用长方形的面积公式得到长方形的面积=$\frac{1}{18}$a2,正方形的边长为$\frac{1}{4}$a,则正方形的面积=$\frac{1}{16}$a2;设圆的半径为r,利用圆的周长公式得到r=$\frac{a}{2π}$,所以圆的半径=$\frac{1}{4π}$a2,可猜得围成圆的面积最大,然后取a=4进行验证.
解答 解:设长方形的宽为x,则长为2x,x+2x=$\frac{1}{2}$a,解得x=$\frac{1}{6}$a,所以长方形的面积=2x•x=2x2=2×($\frac{1}{6}$a)2=$\frac{1}{18}$a2;
正方形的面积=($\frac{1}{4}$a)2=$\frac{1}{16}$a2;
设圆的半径为r,则2πr=a,解得r=$\frac{a}{2π}$,所以圆的半径=π•($\frac{a}{2π}$)2=$\frac{1}{4π}$a2;
结论:围成圆的面积最大.
验证:当a=4时,长方形的面积=$\frac{8}{9}$,正方形的面积=1,圆的面积=$\frac{4}{π}$,
而$\frac{8}{9}$<1<$\frac{4}{π}$,
即圆的面积最大.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. (2)列代数式五点注意:①仔细辨别词义. 列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.

练习册系列答案
相关题目
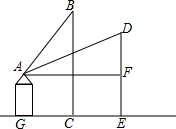 起重机的吊杆与水平线夹角叫倾角,某起重机机身高20米,吊杆倾角是30°时,工作的水平距离AF为10$\sqrt{3}$米,求:当吊杆倾角是60°时,工作的高度BC.
起重机的吊杆与水平线夹角叫倾角,某起重机机身高20米,吊杆倾角是30°时,工作的水平距离AF为10$\sqrt{3}$米,求:当吊杆倾角是60°时,工作的高度BC.