题目内容
10.若|m|=3,|n|=2,$\frac{m}{n}$<0,则3m-2n的值为±13.分析 首先求得m、n的值,然后根据$\frac{m}{n}$<0分类计算即可.
解答 解:∵|m|=3,|n|=2,
∴m=±3,n=±2.
∵$\frac{m}{n}$<0,
∴当m=3时,n=-2;当m=-3时,n=2.
当m=3,n=-2时,原式=3×3-2×(-2)=9+4=13;
当m=-3,n=2时,原式=3×(-3)-2×2=-9-4=-13.
故答案为:±13.
点评 本题主要考查的是绝对值的性质、有理数的加减乘除混合运算,掌握运算法则是解题的关键.

练习册系列答案
相关题目
5.设a是最小的质数,b是最大的负整数,c是绝对值最小的实数,则a,b,c三个数的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.下列说法不正确的是( )
| A. | 平面内两条不想交的直线叫做平行线 | |
| B. | 一条直线的平行线有且只有一条 | |
| C. | 过直线外一点能画一条直线与已知直线平行 | |
| D. | 过直线外一点能画一条直线与已知直线垂直 |
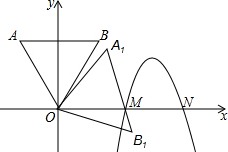 如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3.
如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3.