题目内容
4.(1)分解因式(a2+4)2-16a2(2)解方程组:$\left\{\begin{array}{l}{3x-y=-4}\\{x-2y=-3}\end{array}\right.$.
分析 (1)原式利用平方差公式分解,再利用完全平方公式化简即可;
(2)方程组利用代入消元法求出解即可.
解答 解:(1)原式=( a2+4-4a)( a2+4+4a)=( a-2)2(a+2)2;
(2)由②得:x=-3+2y ③,
把③代入①得,y=1,
把y=1代入③得:x=-1,
则原方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
4. 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )
 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
15.已知(3-2a)x+2=0是关于x的一元一次方程,则|a-$\frac{3}{2}$|一定( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 不确定 |
19.如果方程2xm-1-3y2m+n=1是关于x、y的二元一次方程,那么m、n的值分别为( )
| A. | 1,0 | B. | 2,-3 | C. | 1,-3 | D. | 1,1 |
14.在实数0、-1、$\sqrt{2}$、0.12345中,无理数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
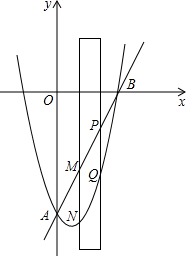 如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).
如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0). (1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°
(1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°