题目内容
19. 如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是②③④.(请填序号)
如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是②③④.(请填序号)
分析 如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.
解答 解:如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.
∵四边形ABCD是平行四边形,
∴AB∥CH,
∴∠A=∠FDH,
在△AFE和△DFH中,
$\left\{\begin{array}{l}{∠A=∠FDH}\\{∠AFE=∠HFD}\\{AF=DF}\end{array}\right.$,
∴△AFE≌△DFH,
∴EF=FH,
∵CE⊥AB,AB∥CH,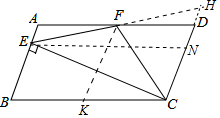
∴CE⊥CD,
∴∠ECH=90°,
∴CF=EF=FH,故②正确,
∵DF=CD=AF,
∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,
∴∠DCF>∠ECF,故①错误,
易证四边形DFKC是菱形,
∴∠DFC=∠KFC,
∵AE∥EK,
∴∠AEF=∠EFK,
∵FE=FC,FK⊥EC,
∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,
∵四边形EBCN是平行四边形,
∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,
∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.
故答案为②③④.
点评 本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a2÷a2=2a2 | C. | (a3)2=a5 | D. | a•a2=a3 |
14.关于x的一元二次方程(m2-1)x2-2(m+1)x+1=0有实数根,则m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m≥-1且m≠1 | D. | m>-1且m≠1 |
4.据统计,2017年春节黄金周7天,杭州共接待中外游客约450万人次,将450万用科学记数法表示,以下表示正确的是( )
| A. | 450×104 | B. | 45.0×105 | C. | 4.50×106 | D. | 4.50×107 |
11.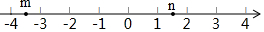 实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
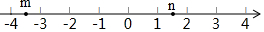 实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )| A. | m>-3 | B. | m<-4 | C. | m>n | D. | m<-n |
8.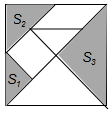 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )| A. | 1:2:3 | B. | 1:$\sqrt{2}$:2 | C. | 1:$\sqrt{2}$:4 | D. | 1:2:4 |