��Ŀ����
2��ij�̳�Ϊ��ӭ�ӡ�6.1��ͯ�ڡ����Ե��ͼ۸�ķ�ʽ����n����ͬ����ߣ�������ĵ���y��Ԫ�������ǰ�ĵ���x��Ԫ������һ�κ�����ϵ�������| ��1�� | ��2�� | ��3�� | ��4�� | �� | ��n�� | |
| ����ǰ����x ��Ԫ�� | x1 | x2=6 | x3=72 | x4 | �� | xn |
| ������y ��Ԫ�� | y1 | y2=4 | y3=59 | y4 | �� | yn |
��1��y��x�ĺ�����ϵʽΪ��x��ȡֵ��ΧΪ��
��2��ij����ߵ���ǰ������108Ԫ���˿���������ʡ��Ԫ��
��3����n����ߵ���ǰ�����ƽ�����۷ֱ�Ϊ$\overline{x}$��Ԫ����$\overline{y}$��Ԫ��������$\overline{y}$��$\overline{x}$�Ĺ�ϵʽ����д���Ƶ����̣�
���� ��1����y=kx+b���ѣ�6��4������72.59������õ�$\left\{\begin{array}{l}{6k+b=4}\\{72k+b=59}\end{array}\right.$���ⷽ���鼴�ɣ�
��2�����ã�1���Ĺ�ϵʽ���y�����ɽ�����⣮
��3�����룺$\overline y$=$\frac{5}{6}$$\overline x$-1������ƽ�����۵Ķ��壬�г�ʽ�Ӽ��㼴�ɣ�
��� �⣺��1����y=kx+b���ѣ�6��4������72.59������õ�$\left\{\begin{array}{l}{6k+b=4}\\{72k+b=59}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{5}{6}}\\{b=-1}\end{array}\right.$
��y=$\frac{5}{6}$x-1��x��$\frac{18}{5}$����
��2����x=108ʱ��y=89��
108-89=19��
��˿���������ʡ��19Ԫ��
��3�����룺$\overline y$=$\frac{5}{6}$$\overline x$-1
֤����y1=$\frac{5}{6}$x1-1��y2=$\frac{5}{6}$x2-1������yn=$\frac{5}{6}$xn-1
��$\overline y$=$\frac{1}{n}$��y1+y2+��+yn��
=$\frac{1}{n}$��$\frac{5}{6}$x1-1+$\frac{5}{6}$x2-1+��+$\frac{5}{6}$xn-1��
=$\frac{1}{n}$$[{\frac{5}{6}��{x_1}+{x_2}+��+{x_n}��-n}]$
=$\frac{1}{n}$$[{\frac{5}{6}n\overline x-n}]$=$\frac{5}{6}$$\overline x$-1��
���� ���⿼��һ�κ�����Ӧ�ã�ƽ�����۵Ķ����֪ʶ������Ĺؼ����������մ���ϵ����ȷ����������ʽ�������п��������ͣ�

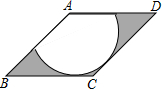 ��ͼ��������ABCD�У���B=45�㣬�Ե�AΪԲ�ĵ�������BC��CD���У�������һ��������������һö���ڣ�����ڲ�����Ӱ����ĸ���Ϊ��������
��ͼ��������ABCD�У���B=45�㣬�Ե�AΪԲ�ĵ�������BC��CD���У�������һ��������������һö���ڣ�����ڲ�����Ӱ����ĸ���Ϊ��������| A�� | 1-$\frac{3\sqrt{2}��}{16}$ | B�� | $\sqrt{2}-\frac{3��}{8}$ | C�� | 1-$\frac{3��}{8}$ | D�� | $\frac{3��}{8}$ |
| A�� | a3+a3=a6 | B�� | 3a2��a2=2a2 | C�� | ��a3��2=a5 | D�� | a•a2=a3 |
| A�� | m��1 | B�� | m��1 | C�� | m��-1��m��1 | D�� | m��-1��m��1 |
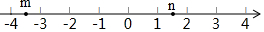 ʵ��m��n�������ϵĶ�Ӧ���λ����ͼ��ʾ�����н�����ȷ���ǣ�������
ʵ��m��n�������ϵĶ�Ӧ���λ����ͼ��ʾ�����н�����ȷ���ǣ�������| A�� | m��-3 | B�� | m��-4 | C�� | m��n | D�� | m��-n |
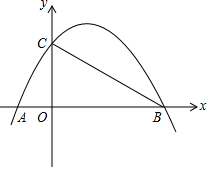 ��֪��A��-1��0������B��4��0������C��y����������ϣ��ҡ�ACB=90�㣮������y=ax2+bx+c����A��B��C���㣬�Ҷ���ΪM��
��֪��A��-1��0������B��4��0������C��y����������ϣ��ҡ�ACB=90�㣮������y=ax2+bx+c����A��B��C���㣬�Ҷ���ΪM��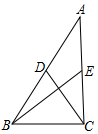 ��ͼ���ڡ�ABC�У�AB=9��AC=7��BE��CDΪ���ߣ���BE��CD����BC=$\sqrt{26}$��
��ͼ���ڡ�ABC�У�AB=9��AC=7��BE��CDΪ���ߣ���BE��CD����BC=$\sqrt{26}$��