题目内容
20.计算:(1)$\sqrt{48}+\sqrt{3}$;
(2)$(\sqrt{\frac{4}{3}}+\sqrt{3})×\sqrt{6}$.
(3)$\sqrt{\frac{2}{5}}-\sqrt{\frac{1}{10}}$;
(4)$\sqrt{12}-\sqrt{3}+\sqrt{\frac{1}{3}}$.
分析 根据二次根式的各种运算法则计算即可.
解答 解:
(1)原式=4$\sqrt{3}$+$\sqrt{3}$,
=5$\sqrt{3}$;
(2)原式=$\frac{\sqrt{24}}{\sqrt{3}}+\sqrt{18}$,
=2$\sqrt{2}$+3$\sqrt{2}$,
=5$\sqrt{2}$;
(3)原式=$\frac{\sqrt{10}}{5}-\frac{\sqrt{10}}{10}$,
=$\frac{\sqrt{10}}{10}$;
(4)原式=2$\sqrt{3}$-$\sqrt{3}$-$\frac{\sqrt{3}}{3}$,
=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了二次根式的有关运算,二次根式的混合运算是二次根式乘法、除法及加减法运算法则的综合运用.学习二次根式的混合运算应注意以下几点:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列二次根式中,与$\sqrt{3}$能合并的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{27}$ | C. | $\sqrt{96}$ | D. | $\sqrt{0.5}$ |
10.下列说法正确的有( )
①每个命题都有逆命题;②互逆命题的真假性一致;③每个定理都有逆定理.
①每个命题都有逆命题;②互逆命题的真假性一致;③每个定理都有逆定理.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |

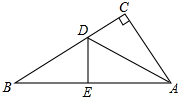 如图,在Rt△ABC中,∠C=90°,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.若CD=6,BD=10,求AC长.
如图,在Rt△ABC中,∠C=90°,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.若CD=6,BD=10,求AC长.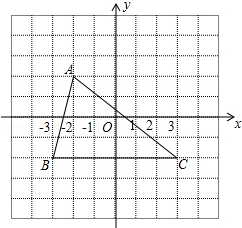 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,