Question

8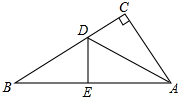．如图，在Rt△ABC中，∠C=90°，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．若CD=6，BD=10，求AC长．

Answer 1

分析 在直角三角形中，可直接应用勾股定理求得BE的长度，再利用勾股定理列出方程解答即可．

解答 解：∵在Rt△ABC中，∠C=90°，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，
∴CD=DE=6，AC=AE，
在Rt△BDE中，BE=$\sqrt{1{0}^{2}-{6}^{2}}=8$，
设AC为x，在Rt△ABC中，可得：x²+（10+6）²=（8+x）²，
解得：x=12，
答：AC的长为12．

点评 本题考查了翻折变换问题；找准相等的量，结合勾股定理求解是解答此类问题的关键．