题目内容
13.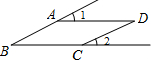 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
分析 先根据同位角相等,两直线平行,由∠1=∠B得到AD∥BC,然后根据平行线的性质求解.
解答 解:∵∠1=∠B,
∴AD∥BC,
∴∠D=∠2=25°.
故选A.
点评 本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.

练习册系列答案
相关题目
3.下列各式:$\frac{1}{5}$(1-x),$\frac{4x}{π-3}$,$\frac{{x}^{2}-{y}^{2}}{2}$,$\frac{1+a}{b}$,$\frac{5{x}^{2}}{y}$,其中分式共有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1. 把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )
 把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )| A. | 148° | B. | 64° | C. | 116° | D. | 136° |
18.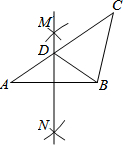 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
5. 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 长方体 | D. | 正方体 |
2.在五张完全相同的卡片上,分别写有数字0,-1,-2,1,3,现从中随机抽取一张,抽到写有负数的卡片的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
3.如果一个多边形的内角和等于720°,则这个多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
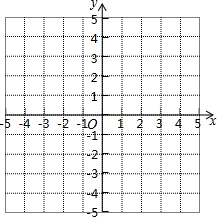 二次函数y=ax2+bx+c(a≠0)的图象与一次函数y1=x+bk的图象交于A(0,1)、B两点,C(1,0)为二次函数图象的顶点.
二次函数y=ax2+bx+c(a≠0)的图象与一次函数y1=x+bk的图象交于A(0,1)、B两点,C(1,0)为二次函数图象的顶点.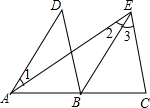 请在括号或横线上,填写下列命题的证明过程中的推理或依据.
请在括号或横线上,填写下列命题的证明过程中的推理或依据.