题目内容
4. 二次函数y=ax2+bx+c(a≠0)的图象与一次函数y1=x+bk的图象交于A(0,1)、B两点,C(1,0)为二次函数图象的顶点.
二次函数y=ax2+bx+c(a≠0)的图象与一次函数y1=x+bk的图象交于A(0,1)、B两点,C(1,0)为二次函数图象的顶点.(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在所给的平面直角坐标系中画出二次函数y=ax2+bx+c(a≠0)的图象和一次函数y1=x+bk的图象;
(3)把(1)中的二次函数y=ax2+bx+c(a≠0)的图象平移后得到新的二次函数y2=ax2+bx+c+m(a≠0,m为常数)的图象,定义新函数f:“当自变量x任取一值时,x对应的函数值分别为y1或y2,如果y1≠y2,函数f的函数值等于y1、y2中的较小值;如果y1=y2,函数f的函数值等于y1(或y2).”当新函数f的图象与x轴有三个交点时,直接写出m的取值范围.
分析 (1)根据题意设抛物线解析式为y=a(x-1)2,把点A(0,1)代入,利用待定系数法即可求得;
(2)求得一次函数的解析式,在同一坐标系中画出图象即可;
(3)二次函数y=ax2+bx+c(a≠0)的图象平移得到新的二次函数y2=ax2+bx+c+m(a≠0,m为常数)的图象的过程中,与x轴的交点由两点变为三点,由三点变为两点,从而求得m的取值范围.
解答 解:(1)∵C(1,0)为二次函数图象的顶点,
∴设抛物线解析式为y=a(x-1)2,
由抛物线过点A(0,1),可得a=1,
∴抛物线解析式为y=x2-2x+1;
(2)由直线过点A(0,1),可得bk=1,
∴一次函数为y1=x+1,
如图: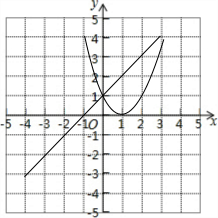
(3)如图所示:当抛物线的顶点在x轴上时,即m=0时,新函数f的图象与x轴有两个个交点,
当抛物线与直线交于(-1,0)时,
0=(-1)2-2×(-1)+1+m,解得m=-4,
即m=-4时新函数f的图象与x轴有两个交点,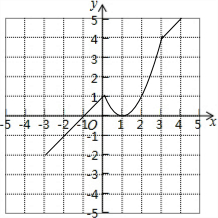
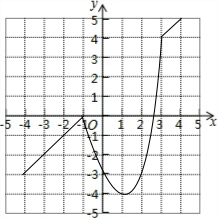
故当新函数f的图象与x轴有三个交点时,m的取值范围为-4<m<0.
点评 本题考查了直线与抛物线解析式的求法、二次函数的图象、抛物线和x轴的交点以及抛物线的相关性质的运用.关键是熟练掌握抛物线顶点式与交点式与性质之间的联系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
19. 如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )
如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )
 如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )
如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )| A. | (1,-2) | B. | (-2,1) | C. | (-2,2) | D. | (2,-2) |
13.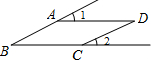 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )
 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
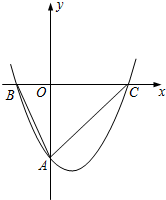 如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0).
如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0). 已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.
已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.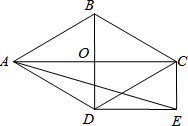 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.