题目内容
10.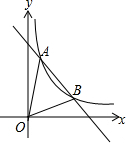 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数图象y=-x+4交于A、B两点,点A的纵坐标为3.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数图象y=-x+4交于A、B两点,点A的纵坐标为3.(1)求反比例函数的解析;
(2)y轴上是否存在一点P,使∠APB=$\frac{1}{2}$∠AOB?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)根据A在y=-x+4上,且点A的纵坐标为3,于是得到A(3,1),由于点A在反比例函数y=$\frac{k}{x}$的图象上,即可得到结论;
(2)根据勾股定理得到OA=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,根据∠APB=$\frac{1}{2}$∠AOB,于是推出点P在以O为圆心,以OA为半径的圆上,得到OP=$\sqrt{10}$,即可得到结论.
解答 解:(1)∵A在y=-x+4上,且点A的纵坐标为3,得
点A(3,1),
∵点A在反比例函数y=$\frac{k}{x}$的图象上,得k=3,
∴反比例函数的解析为:y=$\frac{3}{x}$;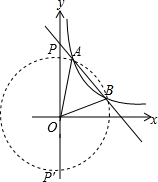
(2)∵A(1,3),
∴OA=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵OA=OB,
∵∠APB=$\frac{1}{2}$∠AOB,
∴点P在以O为圆心,以OA为半径的圆上,
∴OP=$\sqrt{10}$,
∵点P在y轴上,
∴P(0,$\sqrt{10}$)或P(0,$-\sqrt{10}$).
点评 考查了反比例函数与一次函数的交点问题,圆周角定理,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5). 如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.
如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.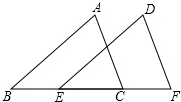 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF. 如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.
如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.