题目内容
5.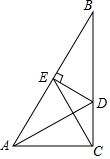 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,AD是△ABC的角平分线,DE⊥
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,AD是△ABC的角平分线,DE⊥AB于点E,连接CE,求CE的长.
分析 由AD是△ABC的角平分线,得到∠EAD=∠CAD,推出∠ACD=∠AED,根据全等三角形的性质得到AE=AC,得到△ACE是等边三角形,于是得到结论.
解答 解:∵AD是△ABC的角平分线,
∴∠EAD=∠CAD,
∵∠ACB=90°,DE⊥AB,
∴∠ACD=∠AED,
在△ACD与△AED中,$\left\{\begin{array}{l}{∠ACD=∠AED=90°}\\{∠EAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED,
∴AE=AC,∵∠B=30°,
∴∠BAC=60°,
∴△ACE是等边三角形,
∴CE=AC=3.
点评 本题考查了全等三角形的判定和性质,角平分线的定义,等边三角形的判定,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
14.在5张形状相同的卡片上,分别写有下列5个命题:
①同位角相等;
②三角形中至少有两个锐角;
③三角形三个外角的和是360°;
④三角形中至少有一个角大于60°;
⑤如果两条直线平行,那么同旁内角的平分线互相垂直.
从中任意抽取一张卡片,抽取到卡片写有真命题的概率是( )
①同位角相等;
②三角形中至少有两个锐角;
③三角形三个外角的和是360°;
④三角形中至少有一个角大于60°;
⑤如果两条直线平行,那么同旁内角的平分线互相垂直.
从中任意抽取一张卡片,抽取到卡片写有真命题的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
15.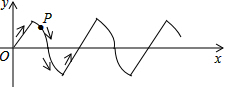 在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
 在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )| A. | ($\frac{2017}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{2017}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (2017,$\sqrt{3}$) | D. | (2017,-$\sqrt{3}$) |
 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由.
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由. 在△ABC中,AD平分∠BAC,DE⊥AB,点F在AC边上,且∠B+∠AFD=180°,求证:BD=DF.
在△ABC中,AD平分∠BAC,DE⊥AB,点F在AC边上,且∠B+∠AFD=180°,求证:BD=DF.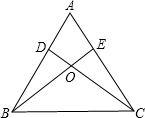 已知:如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,
已知:如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,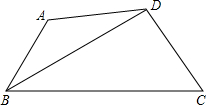 如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,
如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,