题目内容
10. 在△ABC中,AD平分∠BAC,DE⊥AB,点F在AC边上,且∠B+∠AFD=180°,求证:BD=DF.
在△ABC中,AD平分∠BAC,DE⊥AB,点F在AC边上,且∠B+∠AFD=180°,求证:BD=DF.
分析 作DG⊥AC于点G,根据角平分线的性质可以得出DE=DF,在证明△BDF≌△FDG证得BD=DF.
解答  证明:作DG⊥AC于点G.
证明:作DG⊥AC于点G.
∵AD是∠BAC的平分线,DE⊥AB,DG⊥AC,
∴DE=DG.
∵∠B+∠AFD=180°,∠AFD+∠DFC=180°,
∴∠B=∠DFC,
∴在△BDE和△FDG中,
$\left\{\begin{array}{l}{∠B=∠DFC}\\{∠BED=∠DGF=90°}\\{DE=DG}\end{array}\right.$,
∴△BDF≌△FDG(AAS),
∴BD=DF.
点评 本题考查全等三角形的判定与性质以及角的平分线的性质,正确作出辅助线是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列各式中,为完全平方式的是( )
| A. | a2+2b+1 | B. | a2+a-1 | C. | x2-2x+l | D. | x2-2xy+4y2 |
2.三角形三边长分别为15、20、25,则最短边上的高为( )
| A. | 15 | B. | 20 | C. | 24 | D. | 25 |
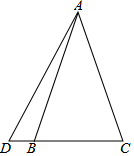 已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为2$\sqrt{10}$.
已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为2$\sqrt{10}$.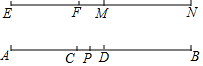 如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )
如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )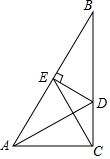 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,AD是△ABC的角平分线,DE⊥
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,AD是△ABC的角平分线,DE⊥