题目内容
若一个一元二次方程的两个根分别是1、-2,请写出一个符合题意的一元二次方程 .
考点:根与系数的关系
专题:开放型
分析:先计算出1与-2的和、积,然后根据根与系数的关系写出满足条件的一元二次方程.
解答:解:∵1+(-2)=-1,
1•(-2)=-2,
∴以1和-2为根的一元二次方程可为x2-x-2=0.
故答案为x2-x-2=0.
1•(-2)=-2,
∴以1和-2为根的一元二次方程可为x2-x-2=0.
故答案为x2-x-2=0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目

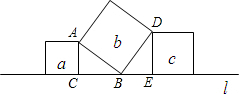 如图,直线l上有三个正方形a、b、c,其中a、c的面积分别为5和11.求正方形b的面积.
如图,直线l上有三个正方形a、b、c,其中a、c的面积分别为5和11.求正方形b的面积.