题目内容
15.解下面三个方程:①$\frac{1}{x}$$+\frac{1}{x-1}$=$\frac{2}{x+1}$;②$\frac{1}{x-9}$=$\frac{2}{x+3}$;③$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$,解的情况是( )| A. | 三个方程都有增根 | B. | 方程①②有解 | ||
| C. | 方程②有解 | D. | 方程③有解 |
分析 分别求出方程的解,然后根据最简公分母判断是否为方程的根,从而得解.
解答 解:①方程两边都乘以x(x-1)(x+1)得,x2-1+x2+x=2(x2-x),
整理得,3x=1,
所以,x=$\frac{1}{3}$,
经检验,x=$\frac{1}{3}$是分式方程的解;
②方程两边都乘以(x-9)(x+3)得,x+3=2(x-9),
解得x=21,
经检验,x=21是分式方程的解;
③方程两边都乘以(x-2)得,1+3(x-2)=x-1,
解得x=2,
检验:当x=2时,x-2=0,
所以,x=2是方程的增根,
综上所述,方程①②有解.
故选B.
点评 本题考查了分式方程的解,解分式方程的一般步骤:①把分式方程化为整式方程,②检验.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
3.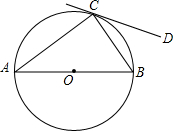 如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
 如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相交或相切 |
5.化简(x+y-1)-1的结果是( )
| A. | $\frac{1}{x+y}$ | B. | $\frac{xy}{x+y}$ | C. | $\frac{y}{xy+1}$ | D. | $\frac{xy+1}{y}$ |
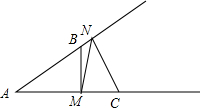 已知∠BAC=30°,AB=3,AC=4,M在AC上,N在AB上,则BM+MN+NC的最小值是$\frac{3}{2}$+2$\sqrt{3}$.
已知∠BAC=30°,AB=3,AC=4,M在AC上,N在AB上,则BM+MN+NC的最小值是$\frac{3}{2}$+2$\sqrt{3}$. 如图,四边形ABDC、DCEF、EFHG是三个正方形,经过努力,你能得出下面几个结论吗?
如图,四边形ABDC、DCEF、EFHG是三个正方形,经过努力,你能得出下面几个结论吗? 如图.在⊙O中,弦AC、BD相交于点E,求证:$\frac{AE}{AB}$=$\frac{DE}{DC}$.
如图.在⊙O中,弦AC、BD相交于点E,求证:$\frac{AE}{AB}$=$\frac{DE}{DC}$.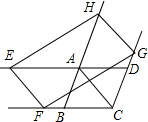 如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.
如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.