题目内容
10. 如图.在⊙O中,弦AC、BD相交于点E,求证:$\frac{AE}{AB}$=$\frac{DE}{DC}$.
如图.在⊙O中,弦AC、BD相交于点E,求证:$\frac{AE}{AB}$=$\frac{DE}{DC}$.
分析 由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠D,又由对顶角相等,易证得△AEB∽△DEC,根据相似三角形的对应边成比例,即可证得结论.
解答 证明:∵∠A与∠D是$\widehat{BC}$所对的圆周角,
∴∠A=∠D,
∵∠AEB=∠DEC,
∴△AEB∽△DEC,
∴$\frac{AE}{DE}=\frac{AB}{DC}$,即$\frac{AE}{AB}=\frac{DE}{DC}$.
点评 此题考查了相似三角形的判定与性质与圆周角定理,比例式通常通过证相似得到,注意掌握数形结合思想的应用.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
1.下列各组条件中,能判断两个直角三角形全等的是( )
| A. | 一组边对应相等 | B. | 两组直角边对应相等 | ||
| C. | 两组锐角对应相等 | D. | 一组锐角对应相等 |
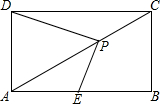 如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.
如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.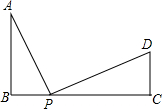 如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.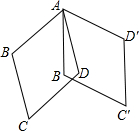 如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$.
如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$. 如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.
如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.