题目内容
7.为解方程(x2-1)2-5(x2-1)+4=0,我们设x2-1=y,则y2=(x2-1)2,则原方程化为y2-5y+4=0,解此方程,得y1=1,y2=4.当y=1时,x2-1=1,x2=2.∴x=±$\sqrt{2}$;
当y=4时,x2-1=4,x2=5,∴x=±$\sqrt{5}$.
∴原方程的解为x1=-$\sqrt{2}$,x2=$\sqrt{2}$,x3=-$\sqrt{5}$,x4=$\sqrt{5}$
在上面的解答过程中,我们把x2-1看成一个整体,用字母y代替(即换元),使得问题简单化.明朗化,解答过程更清晰,这是解决数学问题中的一种重要方法-换元法,仿照上述方法,解答下列问题:
(1)解方程:x4-3x2-4=0.
(2)直角三角形中,两条直角边分别为a,b,且满足(a2+b2)(a2+b2+1)=12,求这个直角三角形的斜边长.
分析 (1)设x2=y,则x4=y2.则方程即可变形为y2-3y-4=0,解方程即可求得y即x2的值;
(2)设斜边为c,根据勾股定理c2=a2+b2代入方程求解即可.
解答 解:(1)设x2=y,x4=y2,则原方程可化为y2-3y-4=0,
解得y1=-1,y2=4.
当y=-1时,x2=-1,舍去;
当y=4时,x2=4,x=±2.
故原方程的解为:x1=2,x2=-2;
(2)设斜边为c,
∵a,b是一个直角三角形两条直角边的长,
∴(a2+b2)(a2+b2+1)=12,根据勾股定理得:c2(c2+1)-12=0
即(c2-3)(c2+4)=0,
∵c2+4≠0,
∴c2-3=0,
解得:c=$\sqrt{3}$或c=-$\sqrt{3}$(舍去).
则直角三角形的斜边长为$\sqrt{3}$.
点评 本题考查了换元法解一元二次方程.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.解下面三个方程:①$\frac{1}{x}$$+\frac{1}{x-1}$=$\frac{2}{x+1}$;②$\frac{1}{x-9}$=$\frac{2}{x+3}$;③$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$,解的情况是( )
| A. | 三个方程都有增根 | B. | 方程①②有解 | ||
| C. | 方程②有解 | D. | 方程③有解 |
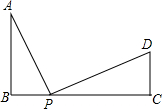 如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.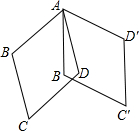 如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$.
如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$.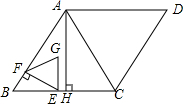 如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.
如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.