题目内容
9. 如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.(1)试找出与∠AGC相等的角,并进行证明;
(2)若AB∥DG,求证;△ACG与△ACE相似;
(3)若OE=BE,求∠AGC的度数.
分析 (1)结论:∠ACE=∠AGC.首先证明AB垂直平分CD,推出AC=AD,∠ACD=∠ADC,因为∠AGC=∠ADC,由此即可证明.
(2)如图2中,由DG∥AB,推出∠AEC=∠CDG=90°,推出CG是直径,推出∠CAG=90°,由此即可证明.
(3)如图3中,连接OC、BC.只要证明△OBC是等边三角形即可解决问题.
解答 解:(1)结论:∠ACE=∠AGC.理由如下:
如图1中,连接AD.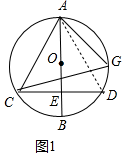
∵AB是直径,AB⊥CD,
∴EC=ED,
∴AD=AC,
∴∠ACE=∠ADC,
∵∠AGC=∠ADC,
∴∠ACE=∠AGC.
(2)证明:如图2中,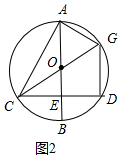
∵DG∥AB,
∴∠AEC=∠CDG=90°,
∴CG是直径,
∴∠CAG=90°,
∵∠CAG=∠AEC=90°,∠AGC=∠ACE,
∴△ACG∽△EAC.
(3)解:如图3中,连接OC、BC.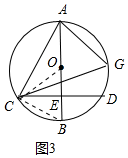
∵OE=EB,CE⊥OB,
∴CO=CB=OB,
∴△OBC是等边三角形,
∴∠B=60°,
∴∠AGC=∠B=60°.
点评 本题考查相似三角形综合题、圆的有关知识、直径的判定和性质、等边三角形的判定和性质、线段的垂直平分线的性质和判定等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,属于中考压轴题.

练习册系列答案
相关题目
1.若x2+2(m-3)x+25是完全平方式,则m的值等于( )
| A. | 3 | B. | -5 | C. | 7 | D. | 8或-2 |
18.关于x的方程(a-2)x2-2x-3=0有一根为-1,则另一根为( )
| A. | -3 | B. | 3 | C. | 2 | D. | 1 |
14.小明做了以下4道计算题,请你帮他检查一下,他一共做对了( ):
①(-1)2007=2007;②0-(-1)=1;③-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$;④$\frac{1}{2}$÷(-$\frac{1}{2}$)=-1.
①(-1)2007=2007;②0-(-1)=1;③-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$;④$\frac{1}{2}$÷(-$\frac{1}{2}$)=-1.
| A. | 1题 | B. | 2题 | C. | 3题 | D. | 4题 |
18.对于二次函数y=2x2-4x-6,下列说法正确的是( )
| A. | 图象的开口向下 | B. | 当x>1时,y随x的增大而减小 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 图象的对称轴是直线x=-1 |
17.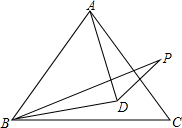 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 无法计算 |
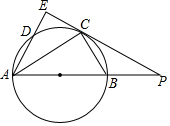 如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2.
如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2. 如图,已知AB∥CD,∠BAE=40°,∠DCE=50°,则∠E=90°.
如图,已知AB∥CD,∠BAE=40°,∠DCE=50°,则∠E=90°.