Question

2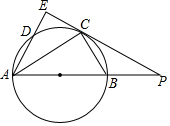．如图，Rt△APE，∠AEP=90°，以AB为直径的⊙，O交PE于C，且AC平分∠EAP．连接BC，PB：PC=1：2．
（1）求证：PE是⊙O的切线；
（2）已知⊙O的半径为$\frac{5}{2}$，求AE的长．

Answer 1

分析 （1）连接OC，由AC平分∠EAP，得到∠DAC=∠OAC，由等腰三角形的性质得到∠CAO=∠ACO，等量代换得到∠DAC=∠ACO，根据平行线的性质得到∠E=∠OCP=90°，于是得到结论；
（2）设PB=x，PC=2x，根据勾股定理得到PC=$\frac{10}{3}$，PB=$\frac{5}{3}$，求得AP=$\frac{20}{3}$，根据相似三角形的性质即可得到结论．

解答 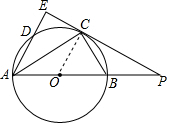解：（1）连接OC，
∵AC平分∠EAP，
∴∠DAC=∠OAC，
∵OA=OC，
∴∠CAO=∠ACO，
∴∠DAC=∠ACO，
∴AE∥OC，
∴∠E=∠OCP=90°，
∴PE是⊙O的切线；

（2）∵PB：PC=1：2，
∴设PB=x，PC=2x，
∵OC²+PC²=OP²，即（$\frac{5}{2}$）²+（2x）²=（$\frac{5}{2}$+x）²，
∴x=$\frac{5}{3}$，
∴PC=$\frac{10}{3}$，PB=$\frac{5}{3}$，
∴AP=$\frac{20}{3}$，
∵OC∥AE，
∴△PCO∽△PEA，
∴$\frac{OC}{AE}=\frac{PO}{AP}$，
∴AE=4．

点评 本题考查了切线的判定，相似三角形的判定和性质，勾股定理，熟记切线的判定是解题的关键．