题目内容
10.解方程组$\left\{\begin{array}{l}{x+\sqrt{2}y=3}\\{2{x}^{2}+{y}^{2}=4}\end{array}\right.$.分析 将方程①移项后两边平方得:2y2=x2-6x+9,与方程②联立消去y后解关于x的一元二次方程,将所求x的值代入方程①求出y的值即可得.
解答 解:依题意 $\left\{\begin{array}{l}{x+\sqrt{2}y=3}&{①}\\{2{x}^{2}+{y}^{2}=4}&{②}\end{array}\right.$
由①得2y2=x2-6x+9 ③,
由②得y2=4-2x2 ④,
将④代入③化简得5x2-6x+l=0,
解得,x1=1,x2=$\frac{1}{5}$,
代入①得y1=$\sqrt{2}$,y2=$\frac{7\sqrt{2}}{5}$,
故原方程的解为:$\left\{\begin{array}{l}{x=1}\\{y=\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{5}}\\{y=\frac{7\sqrt{2}}{5}}\end{array}\right.$.
点评 本题主要考查解高次方程的能力和化归思想的应用,将原方程变形后利用加减或代入的方法消元是解题的关键.

练习册系列答案
相关题目
5.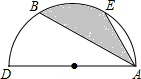 如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )
如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )
 如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )
如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
15.自成都地铁4号线开通以来,成都地铁1、2、4号线线网客流增加明显,再遇到春季糖酒会、桃花节、通勤客流等三股主要客流汇集,2016年3月25日,成都地铁再创单日线网客流历史新高,达到1738200乘次,用科学记数法表示1738200为(保留三个有效数字)( )
| A. | 1.74×106 | B. | 1.73×106 | C. | 17.4×105 | D. | 17.3×105 |
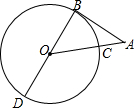 如图,BD为⊙O的直径,AB与⊙O相切于点B,连结AO,AO与⊙O交于点C,若∠A=40°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{13}{9}$π.
如图,BD为⊙O的直径,AB与⊙O相切于点B,连结AO,AO与⊙O交于点C,若∠A=40°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{13}{9}$π.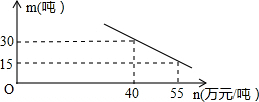 某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.
某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.