题目内容
15.计算:$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}$-$\frac{x+\sqrt{xy}+y}{x\sqrt{x}-y\sqrt{y}}$.分析 先进行二次根式的化简,然后合并.
解答 解:原式=$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}$-$\frac{(x+\sqrt{xy}+y)(x\sqrt{x}+y\sqrt{y})}{(x\sqrt{x}-y\sqrt{y})(x\sqrt{x}-y\sqrt{y})}$
=$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}$-$\frac{{x}^{2}\sqrt{x}+xy\sqrt{y}+{x}^{2}\sqrt{y}+{y}^{2}\sqrt{x}+xy\sqrt{x}+{y}^{2}\sqrt{y}}{{x}^{3}-{y}^{3}}$
=$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}$-$\frac{({x}^{2}+xy+{y}^{2})(\sqrt{x}+\sqrt{y})}{(x-y)({x}^{2}+xy-{y}^{2})}$
=$\frac{x(\sqrt{x}+\sqrt{y})}{y(x-y)}$-$\frac{\sqrt{x}+\sqrt{y}}{x-y}$
=$\frac{(\sqrt{x}+\sqrt{y})(x-y)}{y(x-y)}$
=$\frac{\sqrt{x}+\sqrt{y}}{y}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简与合并.

练习册系列答案
相关题目
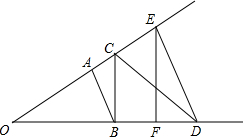 已知A、C、E和B、F、D分别是∠O两边上的点且AB∥ED,BC∥EF,求证:AF∥CD.
已知A、C、E和B、F、D分别是∠O两边上的点且AB∥ED,BC∥EF,求证:AF∥CD.