题目内容
11.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=80°,则∠OAB的大小为50(度).分析 根据矩形的性质求出OA=OB,由等腰三角形的性质和三角形内角和定理即可得出结果.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB,
∴∠OAB=∠OBA=$\frac{1}{2}$(180°-∠AOB)=$\frac{1}{2}$(180°-80°)=50°;
故答案为:50.
点评 本题考查了矩形的性质,等腰三角形的判定与性质,三角形内角和定理;熟练掌握矩形的性质,证出OA=OB是解决问题的关键.

练习册系列答案
相关题目
20. 如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
 如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
2.将一个正方体沿某些棱展开后,能够得到的平面图形是( )
| A. |  | B. |  | C. |  | D. |  |
18. a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )
 a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )| A. | -a-b | B. | a+b | C. | a-b | D. | b-a |
 x的方程x2-(m+2)x+(
x的方程x2-(m+2)x+( 2m-1)=0.
2m-1)=0.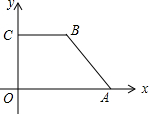 如图,在直角坐标系中,点A、C分别在x轴、y轴上,CB∥OA,CB=8,OC=8,OA=16.
如图,在直角坐标系中,点A、C分别在x轴、y轴上,CB∥OA,CB=8,OC=8,OA=16.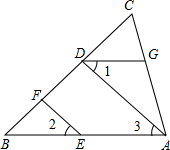 如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.
如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.