题目内容
17．（1）解不等式组：$\left\{\begin{array}{l}{\frac{x-2}{4}+2≥x}&{①}\\{1-3（x-2）＜9-x}&{②}\end{array}\right.$（2）因式分解：x2（2x-5）+4（5-2x）
分析 （1）分别求出各不等式的解集，再求出其公共解集即可；
（2）先提取公因式，再利用平方差公式即可得出结论．
解答 解：（1）由①得，x＞-1，由②得，x≤2，故不等式组的解集为：-1＜x≤2；
（2）原式=（2x-5）（x2-4）=（2x-5）（x+2）（x-2）．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
8．
如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD的周长是（ ）
如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD的周长是（ ）| A． | 16 cm | B． | 18 cm | C． | 20 cm | D． | 21 cm |
9．当b＞0时，一次函数y=x+b的图象大致是（ ）
| A． |  | B． |  | C． |  | D． |  |
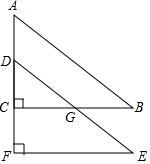如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6cm，将△ABC沿着AC方向平移2cm得△DEF，DE交BC于点G，则四边形CGEF的面积为10$\sqrt{3}$cm2．
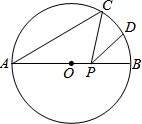如图，AB是⊙O的直径，AB=10，∠A=40°，点D为弧BC的中点，点P是直径AB上的一个动点，PC+PD的最小值为5$\sqrt{3}$．