题目内容
10.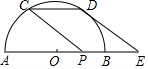 如图,已知半圆O的直径AB为8,P为OB的中点,C为半圆上一点,连结CP,若将CP沿射线AB方向平移至DE,若DE恰好与⊙O相切于点D,则平移的距离为$\sqrt{33}$-1.
如图,已知半圆O的直径AB为8,P为OB的中点,C为半圆上一点,连结CP,若将CP沿射线AB方向平移至DE,若DE恰好与⊙O相切于点D,则平移的距离为$\sqrt{33}$-1.
分析 如图,过OM⊥CD于M,连接OD,则CM=DM,由DE是⊙O的切线,得到OD⊥DE,由平移的性质得到CD∥PE,CD=PE,根据平行线的性质得到∠1=∠2,根据相似三角形的性质即可得到结论.
解答 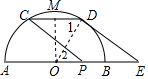 解:如图,过OM⊥CD于M,连接OD,
解:如图,过OM⊥CD于M,连接OD,
则CM=DM,
∵DE是⊙O的切线,
∴OD⊥DE,
∵将CP沿射线AB方向平移至DE,
∴CD∥PE,CD=PE,
∴∠1=∠2,
∵∠DMO=∠ODE=90°,
∴△DMO∽△ODE,
∴$\frac{MO}{OD}=\frac{OD}{OE}$,
设CD=x,
∴$\frac{\frac{1}{2}x}{4}$=$\frac{4}{x+2}$,
∴x=$\sqrt{33}$-1,
∴平移的距离为$\sqrt{33}$-1.
故答案为:$\sqrt{33}$-1.
点评 本题考查了切线的性质,平移的性质,相似三角形的判定和性质,掌握的作出辅助线是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.下列基本几何体中,三视图都是相同图形的是( )
| A. |  圆柱 | B. |  三棱柱 | C. |  球 | D. |  长方体 |
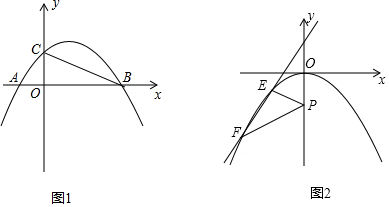
19.在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
(1)求抛物线的解析式;
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥$\frac{1}{2}$S△BOC,求xQ的取值范围;
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,-1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.
| x | … | -1 | 0 | 3 | … |
| y | … | 0 | 3/2 | 0 | … |
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥$\frac{1}{2}$S△BOC,求xQ的取值范围;
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,-1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.

 图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字.
图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字.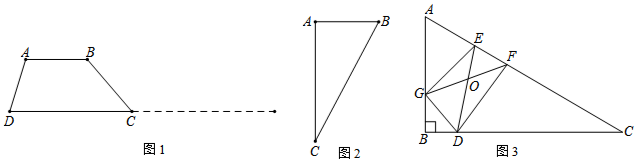
 如图是一个正方体的平面展开图,试问:将其折叠成正方体后,红、黄、绿的对面分别是什么面?
如图是一个正方体的平面展开图,试问:将其折叠成正方体后,红、黄、绿的对面分别是什么面?