化简:$\sqrt{^{2}}$+|tan50°-tan60°| 题目和参考答案——青夏教育精英家教网—

题目内容

5．化简：$\sqrt{（tan30°-tan50°）^{2}}$+|tan50°-tan60°|

分析原式利用二次根式性质，绝对值的代数意义，以及特殊角的三角函数值计算即可得到结果．

解答解：原式=|$\frac{\sqrt{3}}{3}$-tan50°|+|tan50°-$\sqrt{3}$|=tan50°-$\frac{\sqrt{3}}{3}$-tan50°+$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$．

点评此题考查了二次根式的性质与化简，以及特殊角的三角函数值，熟练掌握二次根式性质及绝对值的代数意义是解本题的关键．

练习册系列答案

相关题目

15．

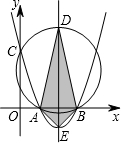如图，开口向上的抛物线y=$\frac{1}{a}$（x-a）（x-3a）的顶点为E，与x轴相交于点A、B两点，与y轴交于点C，经过A、B、C三点的圆与抛物线的对称轴在x轴上方的交点为D．已知圆的半径是$3\sqrt{5}$，则四边形AEBD的面积是27+9$\sqrt{5}$．

13．如图所示，在等边△OAB中，OB=4，点A在第一象限．
（1）点A的坐标为（2，2$\sqrt{3}$）；
（2）在坐标平面内存在3个点C，使得以A、O、B、C为顶点的四边形为平行四边形；
（3）在（2）的条件下，若点C为第一象限的点，且点P从点O出发，以每秒1个单位的速度沿x轴的正方向移动，点Q从点B同时出发，以同样的速度沿射线BC的方向移动，试判断△APQ的形状；
（4）当△APQ周长最小时，求出直线PQ的关系式．

20．已知是a整数，且-3＜a＜4，则表示a的所有整数的积是0．

10．

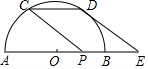如图，已知半圆O的直径AB为8，P为OB的中点，C为半圆上一点，连结CP，若将CP沿射线AB方向平移至DE，若DE恰好与⊙O相切于点D，则平移的距离为$\sqrt{33}$-1．

17．单项式-$\frac{2{a}^{4}b{c}^{2}}{3}$的系数与次数分别是（　　）

14．$\sqrt{5}$介于下列哪两个整数之间（　　）

15．有一块长25cm，宽15cm的长方形硬纸板，如果在纸板的四个角上各截去一个相同大小的小正方形，然后把四边折起来，做成一个底面积为231cm²的无盖长方体盒子，求截去的小正方形的边长．

试题分类