题目内容
在直角△ABC纸片中，已知∠B=90°，AB=6，BC=8，折叠纸片使AB边与AC边重合，B点落在点E上，折痕为AD，则BD的长为（ ）| A、3 | B、4 | C、5 | D、6 |
考点：翻折变换（折叠问题）
专题：
分析：根据勾股定理，可得AC的长，根据折叠得到的图形与原图形是全等图形，可得对应的边相等，根据勾股定理，可得答案．
解答：解：设BD=x，
在Rt△ABC中，由勾股定理，得
AC=
=
=10．
折叠纸片使AB边与AC边重合，B点落在点E上，
AE=AB=6，BD=CE=x，
EC=AC-AE=10-6=4．
由线段的和差，得
DC=BC-BD=8-x．
在Rt△CED中，由勾股定理，得
DE2+CE2=DC2
x2+42=（8-x）2
x=3，
故选：A．
在Rt△ABC中，由勾股定理，得
AC=
| AB2+BC2 |
| 62+82 |
折叠纸片使AB边与AC边重合，B点落在点E上，
AE=AB=6，BD=CE=x，
EC=AC-AE=10-6=4．
由线段的和差，得
DC=BC-BD=8-x．
在Rt△CED中，由勾股定理，得
DE2+CE2=DC2
x2+42=（8-x）2
x=3，
故选：A．
点评：本题考查了折叠问题，折叠得到的图形与原图形是全等图形．
练习册系列答案
相关题目
函数y=kx-1.5的图象经过点（1，-2），则k的值为（ ）
| A、0.5 | B、-0.5 |
| C、2 | D、-2 |
使分式
有意义的x的取值范围是（ ）
| x |
| x-2 |
| A、x=2 | B、x≠2 |
| C、x=-2 | D、x≠-2 |
在①a4•a2②（-a2）3③a12÷a2④a2•a3⑤a3+a3中，计算结果为a6的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
把方程
-0.5=
的分母化为整数，正确的是（ ）
| 0.5x-0.01 |
| 0.2 |
| 0.4x-0.6 |
| 1.2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
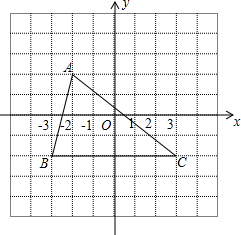如图，△ABC在直角坐标系中，