Question

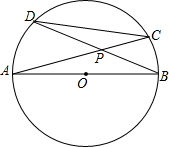如图，⊙O的直径AB，CD是⊙O的弦，AC与BD相交于点P，若∠BPC=30°，CD=4，求AB．

Answer 1

考点：相似三角形的判定与性质,圆周角定理,特殊角的三角函数值

专题：

分析：根据圆周角定理，可得出△CPD和△BPA的两组对应角相等，由此可判定两个三角形相似，可求得

CD

AB

=

PC

PB

，连接BC，则∠BCP=90°，且∠BPC=30°可求得

PC

PB

，代入可求得AB．

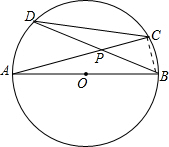解答：解：
连接BC，
∵AB为直径，
∴∠BCP=90°，
∴∠BPC=30°，
∴

CP

PB

=cos∠BPC=cos30°=

3

2

，
∵∠C=∠B，∠D=∠A，（同弧所对的圆周角相等）
∴△CPD∽△BPA，
∴

CD

AB

=

PC

PB

=

3

2

，
且CD=4，
∴

4

AB

=

3

2

，解得AB=

8 3

3

．

点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的判定方法是解题的关键，注意利用特殊角的三角函数找到线段的比例．