题目内容
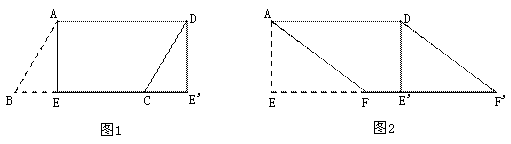
(1)如图1,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′ 的位置,拼成四边形AFF′D.
① 求证四边形AFF′D是菱形;
② 求四边形AFF′D两条对角线的长.

(1)C;
(2)①由AF 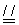 DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
②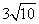 和
和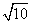 .
.
【解析】
试题分析:(1)由平移的性质得到AE 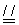 DE′,故四边形AEE′D是平行四边形,又AE⊥BC,得到∠AEE′=90°,所以四边形AEE′D是矩形,故C选项正确;
DE′,故四边形AEE′D是平行四边形,又AE⊥BC,得到∠AEE′=90°,所以四边形AEE′D是矩形,故C选项正确;
(2)①由AF 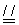 DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
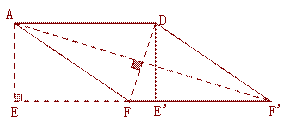
② 如图,连接AF′,DF ,在Rt△AEF′中,可以得到AF′=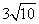 ,在Rt△DFE′中,可以得到DF=
,在Rt△DFE′中,可以得到DF=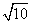 ,故四边形AFF′D两条对角线的长分别是
,故四边形AFF′D两条对角线的长分别是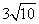 和
和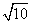 .
.
试题解析:(1)由平移知:AE DE′,∴四边形AEE′D是平行四边形,又AE⊥BC,∴∠AEE′=90°,∴四边形AEE′D是矩形,∴C选项正确;
DE′,∴四边形AEE′D是平行四边形,又AE⊥BC,∴∠AEE′=90°,∴四边形AEE′D是矩形,∴C选项正确;
(2)① ∵AF 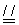 DF′,∴四边形AFF′D是平行四边形,∵AE=3,EF=4 ,∠E=90°,∴AF=5,∵AD=5 ,∴AD=AF , ∴四边形AFF′D是菱形;
DF′,∴四边形AFF′D是平行四边形,∵AE=3,EF=4 ,∠E=90°,∴AF=5,∵AD=5 ,∴AD=AF , ∴四边形AFF′D是菱形;
② 如下图,连接AF′,DF ,在Rt△AEF′中,AE=3,EF′=9, ∴AF′=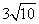 ,在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=
,在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=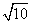 ,∴四边形AFF′D两条对角线的长分别是
,∴四边形AFF′D两条对角线的长分别是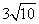 和
和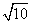 .
.

【难度】一般

 的图象经过点(2,-5),则
的图象经过点(2,-5),则 = .
= .
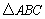 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =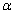 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作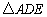 ,使AE=AD,
,使AE=AD,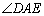 +
+ =180°.
=180°.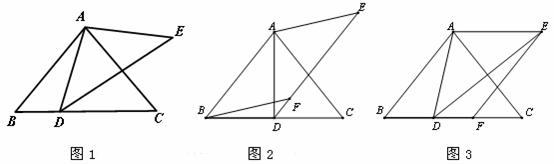

 ;
;
