题目内容
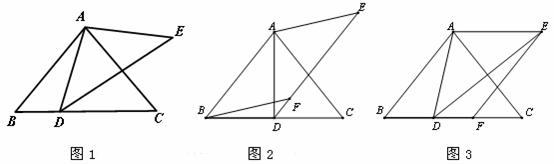
如图1,在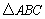 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =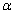 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作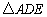 ,使AE=AD,
,使AE=AD,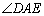 +
+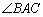 =180°.
=180°.
(1)直接写出∠ADE的度数(用含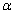 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
(1)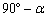
 (2)①证明:∵四边形ABFE是平行四边形,
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥E F.
F.
∴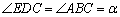 .
.
由(1)知,∠ADE = 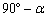 ,
,
∴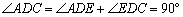 .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =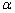 ,
,
∴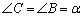 .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴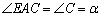 .
.
由(1)知,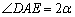 ,
,
∴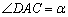 .
.
∴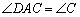 .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
【解析】
试题分析:(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
试题解析:(1)∠ADE = 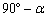 .
.
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥E F.
F.
∴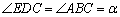 .
.
由(1)知,∠ADE = 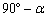 ,
,
∴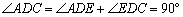 .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =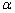 ,
,
∴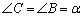 .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴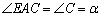 .
.
由(1)知,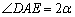 ,
,
∴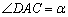 .
.
∴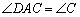 .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
【难度】较难

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案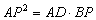 ;
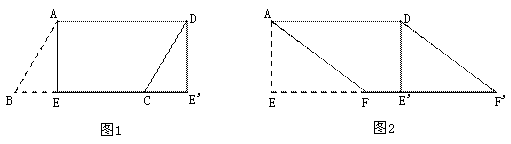
; D恰好与点B重合,点C落在点E的位置上,求此时∠BEP的余切值.
D恰好与点B重合,点C落在点E的位置上,求此时∠BEP的余切值.


 四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.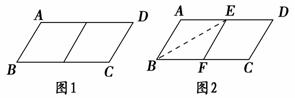

 +|1-
+|1- |+
|+ .
.