题目内容
4.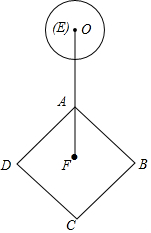 如图,边长为4cm的正方形ABCD,点F为正方形的中点,点E在FA的延长线上,EA=4cm,⊙O的半径为1cm,圆心O从点E出发向点F运动,小明发现:当EO满足①3<EO<5;②3≤EO≤5;③EO=4+$\sqrt{2}$;④EO=4+$3\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点,你认为小明探究的结论中正确的有( )
如图,边长为4cm的正方形ABCD,点F为正方形的中点,点E在FA的延长线上,EA=4cm,⊙O的半径为1cm,圆心O从点E出发向点F运动,小明发现:当EO满足①3<EO<5;②3≤EO≤5;③EO=4+$\sqrt{2}$;④EO=4+$3\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点,你认为小明探究的结论中正确的有( )| A. | ①③ | B. | ②③ | C. | ②④ | D. | ①③④ |
分析 如图1中,当⊙O经过点A时,易知OE=3或5,当3<OE<5时,⊙O与正方形ABCD的边只有两个公共点,如图2中,当⊙O与正方形ABCD的边相切时,设切点为M、N,连接OM.易知OA=$\sqrt{2}$,此时OE=4+$\sqrt{2}$,由此即可判断.
解答 解:如图1中,当⊙O经过点A时,易知OE=3或5,
∴当3<OE<5时,⊙O与正方形ABCD的边只有两个公共点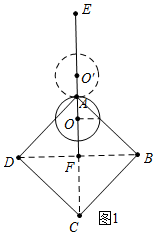
如图2中,当⊙O与正方形ABCD的边相切时,设切点为M、N,连接OM.
易知OA=$\sqrt{2}$,此时OE=4+$\sqrt{2}$,
∴当OE=4+$\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点.
综上所述,当3<OE<5或OE=4+$\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点,
故①③正确,
故选A.
点评 本题考查直线与圆的位置关系、正方形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.下列各式,运算正确的是( )
| A. | 3$\sqrt{3}$-$\sqrt{3}$=3 | B. | 2+$\sqrt{3}$=2$\sqrt{3}$ | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
5.近似数5.0×102精确到( )
| A. | 十分位 | B. | 个位 | C. | 十位 | D. | 百位 |
14.下列关于正方形的叙述,正确的是( )
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
 如图,直线y=ax与双曲线y=$\frac{k}{x}$(x>0)交于点A(1,2),则不等式ax>$\frac{k}{x}$的解集是x>1.
如图,直线y=ax与双曲线y=$\frac{k}{x}$(x>0)交于点A(1,2),则不等式ax>$\frac{k}{x}$的解集是x>1.