题目内容
16．平行四边形ABCD中，∠A比∠B大40°，则∠D的度数为70°．分析 根据平行四边形的对角相等，邻角之和为180°，即可求出该平行四边形各个内角的度数．
解答 解：如图所示：
∵四边形ABCD是平行四边形，
∴∠B=∠D，∠A+∠B=180°，
又∵∠A-∠B=40°，
∴∠A=110°，∠B=70°，
∴∠D=∠B=70°．
故答案为：70°．
点评 本题考查了平行四边形的性质，解题关键是掌握平行四边形的对角相等，邻角之和为180°，难度适中．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7．
如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是（ ）
如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
4．
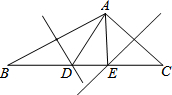如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）
如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）| A． | 16 | B． | 18 | C． | 24 | D． | 32 |
1．在函数y=$\sqrt{2+x}$中，自变量x的取值范围是（ ）
| A． | x≥-2 | B． | x≤-2 | C． | x＞-2 | D． | x＜-2 |
8．下列等式一定成立的是（ ）
| A． | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | B． | $\frac{{\sqrt{7}}}{{\sqrt{5}}}=\sqrt{\frac{7}{5}}$ | C． | $\sqrt{x^2}=\sqrt{x}•\sqrt{x}$ | D． | $\sqrt{{{（π-4）}^2}}$=π-4 |
6．下列命题中，假命题是（ ）
| A． | 对顶角相等 | |
| B． | 等角的补角相等 | |
| C． | 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行 | |
| D． | 如果一个角的两边分别平行于另一个角的两边，那么这两个角相等 |