题目内容
6.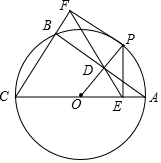 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.(1)求证:OD=OE;
(2)求证:PF是⊙O的切线;
(3)若∠POC=120°,AC=12,将扇形POA围成一个圆锥的侧面,求该圆锥的高.
分析 (1)通过全等三角形△OAD≌△OPE的对应边相等证得结论;
(2)欲证明PF是⊙O的切线,只需推知OP⊥PF即可;
(3)易得∠POA=60°,设所求圆锥的高h,底面半径为r,结合弧长公式和圆锥的侧面展开图进行解答.
解答  证明:(1)∵OD⊥BA于D,PE⊥AC于E,OA=OP,
证明:(1)∵OD⊥BA于D,PE⊥AC于E,OA=OP,
∴在Rt△OAD和Rt△OPE中,$\left\{\begin{array}{l}{∠ADO=∠PEO}\\{∠AOD=∠POE}\\{OA=OP}\end{array}\right.$,
∴△OAD≌△OPE,
∴OD=OE.
(2)由(1)得OD=OE,
∴∠ODE=∠OED,又AC是⊙O的直径,
∴∠ABC=90°,AB⊥BC,
∵OD⊥BC,
∴CB∥OD,
∴∠ODE=∠CFE,
∴∠CFE=∠CEF,从而CE=CF,
连接CP,则∠FCP=∠ACP,
∴CP是线段EF的垂直平分线,
∴PE=PF,
∴△CPE≌△CPF,
∴∠CFP=∠CEP=90°,
∴四边形BDPF是矩形,
∴OP⊥PF,
∴PF是⊙O的切线.
(3)若∠COP=120°,AC=12,则∠POA=60°,
设所求圆锥的高h,底面半径为r,由 $\frac{60π•6}{180}$=2πr,r=1,h=$\sqrt{{6}^{2}-{1}^{1}}$=$\sqrt{35}$.
点评 本题考查了切线的判定与性质、吹径定理以及圆锥的计算等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
17.下列等式中不一定成立的是( )
| A. | $\frac{y}{x}=\frac{xy}{x^2}$ | B. | $\frac{y}{x}=\frac{πy}{πx}$ | C. | $\frac{y}{x}=\frac{yz}{xz}$ | D. | $\frac{y}{x}=\frac{{y({{x^2}+2})}}{{x({{x^2}+2})}}$ |
11.有下列四种说法:
①所有的等边三角形都全等;
②两个三角形全等,它们的最大边是对应边;
③两个三角形全等,它们的对应角相等;
④对应角相等的三角形是全等三角形.
其中正确的说法有 ( )
①所有的等边三角形都全等;
②两个三角形全等,它们的最大边是对应边;
③两个三角形全等,它们的对应角相等;
④对应角相等的三角形是全等三角形.
其中正确的说法有 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.|a|=a,则有理数a为( )
| A. | 正数 | B. | 负数 | C. | 正数和0 | D. | 负数和0 |
15.在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠BAD=120°,则菱形ABCD的周长是( )
| A. | 15 | B. | 16 | C. | 18 | D. | 20 |
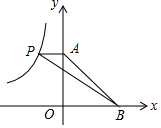 如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.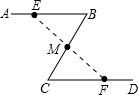 如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?
如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么? 已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题:
已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题: