题目内容
15.在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠BAD=120°,则菱形ABCD的周长是( )| A. | 15 | B. | 16 | C. | 18 | D. | 20 |
分析 作出图形,连接AC、BD,根据菱形的对角线互相垂直平分可得AC⊥BD,OB=$\frac{1}{2}$BD,菱形的对角线平分一组对角求出∠BAO=60°,再求出AB,然后根据菱形的周长等于边长的4倍计算即可得解.
解答  解:如图,连接AC、BD,
解:如图,连接AC、BD,
在菱形ABCD中,AC⊥BD,OB=$\frac{1}{2}$BD=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
∵∠BAD=120°,
∴∠BAO=60°,
在Rt△AOB中,AB=OB÷$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$÷$\frac{\sqrt{3}}{2}$=4,
所以,菱形ABCD的周长=4×4=16.
故选B.
点评 本题考查了菱形的性质,主要利用了菱形的对角线互相垂直平分,菱形的对角线平分一组对角的性质,熟练掌握性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
7.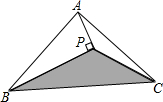 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )| A. | 10cm2 | B. | 12cm2 | C. | 16cm2 | D. | 20cm2 |
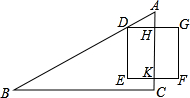 在《九章算术》“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木,问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,向西行1775步到B处正好看到A处的树木(即点D在直线AB上),小城的边长为多少步,若设小城的边长为2x 步,则可列方程为$\frac{20}{20+14+2x}$=$\frac{x}{1775}$.
在《九章算术》“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木,问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,向西行1775步到B处正好看到A处的树木(即点D在直线AB上),小城的边长为多少步,若设小城的边长为2x 步,则可列方程为$\frac{20}{20+14+2x}$=$\frac{x}{1775}$.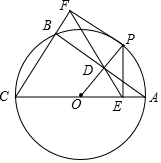 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.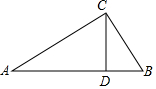 如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求: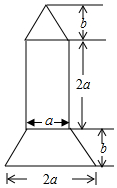 2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空.同学们倍受鼓舞,某同学绘制了如图所示的火箭模型截面图,下面是梯形,中间是长方形,上面是三角形.
2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空.同学们倍受鼓舞,某同学绘制了如图所示的火箭模型截面图,下面是梯形,中间是长方形,上面是三角形.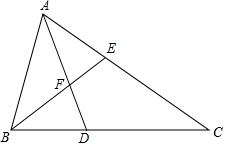 如图,在△ABC中,AD平分∠BAC,BE平分∠ABC,AD、BE相交于点F,且AB+BD=AC.
如图,在△ABC中,AD平分∠BAC,BE平分∠ABC,AD、BE相交于点F,且AB+BD=AC.