题目内容
3.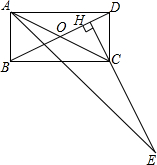 如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.
如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.
分析 由矩形的性质可得∠DOC=2∠DAO,∠HCO=∠CAE+∠E,结合角平分线的定义可求得∠E=∠CAE,可证明CE=AC,结合矩形的性质可得CE=BD.
解答 解:CE=BD,理由如下:
:∵四边形ABCD为矩形,
∴AC=BD,∠BAD=90°,OA=OD,
∴∠HOC=2∠DAO,
又∵CH⊥BD,
∴∠HCO+∠HOC=90°,
∵∠HCO=∠CAE+∠E,
∴2∠DAO+∠CAE+∠E=90°,
又∵AE平分∠BAD,
∴∠DAO+∠CAE=$\frac{1}{2}$∠BAD=45°,
∴2∠DAO+∠CAE+∠E=45°+∠DAO+∠E=90°,
∴∠DAO+∠E=45°,
又∵∠DAO+∠CAE=45°,
∴∠CAE=∠E,
∴CE=AC,
∴CE=BD.
点评 本题主要考查矩形的性质,掌握矩形的四个角都是直角、对角线互相平分且相等是解题的关键,注意三角形外角性质的应用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目