题目内容
11.观察下列勾股数3、4、5;5、12、13;7、24、25;9、40、41;…;a、b、c.根据你发现的规律,回答下列问题:(1)a=17时,求b、c的值;
(2)a=2n+1时,求b、c的值.
分析 (1)仔细观察可发现给出的勾股数中,斜边与较大的直角边的差是1,根据此规律及勾股定理公式不难求得b,c的值.
(2)根据第一问发现的规律,代入勾股定理公式中即可求得b、c的值.
解答 解:(1)观察得给出的勾股数中,斜边与较大直角边的差是1,即c-b=1
∵a=17,a2+b2=c2,
∴172+b2=(b+1)2,
∴b=144,
∴c=145;
(2)通过观察知c-b=1,
∵(2n+1)2+b2=c2,
∴c2-b2=(2n+1)2,
(b+c)(c-b)=(2n+1)2,
∴b+c=(2n+1)2,
∵c=b+1,
∴2b+1=(2n+1)2,
∴b=2n2+2n,c=2n2+2n+1.
点评 此题主要考查学生对勾股数及规律题的综合运用能力,解题的关键是:通过观察知c-b=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
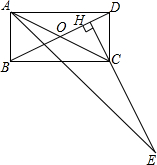 如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.
如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.