题目内容
18.“$\sum_{\;}^{\;}$”是数学上求和符号,$\sum_{n=1}^{10}$n表示求连续的自然数从1到10的和,即$\sum_{n=1}^{10}$n=1+2+3+…+10,已知$\sum_{n=1}^{m}$n=820,求(xmy)•(xm-1y2)•(xm-2y3)•…•(xym)的值.分析 已知等式利用题中的新定义求出m的值,进而求出1+2+…+m的值,原式利用同底数幂的乘法法则计算,将求出1+2+…+m的值代入计算即可求出值.
解答 解:根据题意得:$\sum_{n=1}^{m}$n=$\frac{(m+1)m}{2}$=820,
解得:m=40或m=-41(舍去),
∴1+2+…+m=$\frac{m(m+1)}{2}$=820,
则原式=(xy)820.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.在下列各数中,最小的数是( )
| A. | 1.00×10-9 | B. | 9.99×10-8 | C. | 1.002×10-8 | D. | 9.999×10-7 |
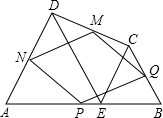 如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )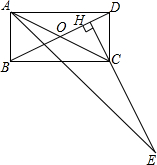 如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.
如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.