��Ŀ����
14��[�����龳]���ɶ�����һ�����ϵ���ѧ���������кܶ���֤���������ҹ�������ѧ����ˬ������ͼ���������������֤����������ѧ�һ���������ѡ���ѧ��ϵ�������ɶ�������������������Ϊ�����������������ˡ����е�һ�Ρ�̸���������ԣ�
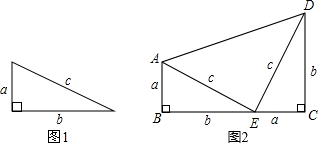
[��������]�������ͼ1�е�ֱ���������������ɶ�����
[����֤��]��ͼ1�е�ֱ��������Ϊ������������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc�������ΰ���ͼ��ʾ�ķ�ʽ���ã���������֮�������ε�����һ����ǵĶ��㣨��ͼ2������������ͼ2����֤���ɶ�����
[֪ʶ��չ]����ͼ2�е�ֱ�����Σ����ǿ���֤��$\frac{a+b}{c}$��$\sqrt{2}$����֤���������£�
��BC=a+b��AD=$\sqrt{2}c$
�֡���ֱ������ABCD�У���BCAD�����С��ϵ������BC��AD
��$\frac{a+b}{c}$$��\sqrt{2}$��
���� ��1�����ݹ��ɶ��������ּ���������������
��2������SAS��֤��ABE�ա�ECD���ɵö�Ӧ����ȣ����90��Ľǣ���֤��AED=90�㣬�������������������ֱ�������ε�����ͣ���֤a2+b2=c2��
��3����ֱ������ABCD�У�BC��AD��������֤��AED��ֱ�������Σ���ô���ù��ɶ�����AD=$\sqrt{2}$c���Ӷ���֤ $\frac{a+b}{c}$��$\sqrt{2}$��
��� �⣺��1�����ɶ��������κ�һ��ֱ���������У�����ֱ�DZ߳���ƽ��֮��һ������б�߳���ƽ����
��2�����ֱ�������ε���ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����ôa2+b2=c2��
��Rt��ABE��Rt��ECD��
���AEB=��EDC��
�֡ߡ�EDC+��DEC=90�㣬
���AEB+��DEC=90�㣻
���AED=90�㣻
S����ABCD=SRt��ABE+SRt��DEC+SRt��AED=$\frac{1}{2}$��a+b����a+b��=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2��
$\frac{1}{2}$��a2+2ab+b2��=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2��
������a2+b2=c2��
��3����AD=$\sqrt{2}$c��BC��AD��
��a+b��$\sqrt{2}$c���� $\frac{a+b}{c}$��$\sqrt{2}$��
�ʴ�Ϊ��$\sqrt{2}c$��BC��AD
���� �����˹��ɶ�����֤��������������ȫ�������ε��ж������ʡ�����ָ�����ɶ�����֪ʶ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�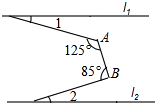 ��ͼ��ֱ��l1��l2����A=125�㣬��B=85�㣬���1+��2���ڣ�������
��ͼ��ֱ��l1��l2����A=125�㣬��B=85�㣬���1+��2���ڣ�������| A�� | 40�� | B�� | 35�� | C�� | 36�� | D�� | 30�� |
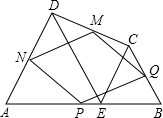 ��ͼ�����ı���ABCD�У�E��AB�ϵ�һ�㣬��ADE�͡�BCE���ǵȱ������Σ���P��Q��M��N�ֱ�ΪAB��BC��CD��DA���е㣬���ı���MNPQ�ǣ�������
��ͼ�����ı���ABCD�У�E��AB�ϵ�һ�㣬��ADE�͡�BCE���ǵȱ������Σ���P��Q��M��N�ֱ�ΪAB��BC��CD��DA���е㣬���ı���MNPQ�ǣ�������| A�� | �������� | B�� | ���� | C�� | ���� | D�� | ������ |
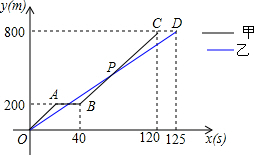 ��800���ܲ����Թ����У����������˶�Աͬʱ���ܣ����ܳ�200��ʱ�ײ���ˤ��������Ѹ���������ٴ�Ͷ������������ճ�Խ��ȡ������ɼ���ͼ�зֱ��ʾ�ס��������˶�Ա���ܵ�·��y��m�������ʱ��x��s��֮��Ĺ�ϵ��
��800���ܲ����Թ����У����������˶�Աͬʱ���ܣ����ܳ�200��ʱ�ײ���ˤ��������Ѹ���������ٴ�Ͷ������������ճ�Խ��ȡ������ɼ���ͼ�зֱ��ʾ�ס��������˶�Ա���ܵ�·��y��m�������ʱ��x��s��֮��Ĺ�ϵ��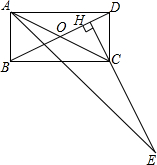 ��ͼ���ھ���ABCD�У���H�ڶԽ���BD�ϣ�HC��BD��HC���ӳ��߽���BAD��ƽ�����ڵ�E���Բ���CE��BD֮���������ϵ��˵�����ɣ�
��ͼ���ھ���ABCD�У���H�ڶԽ���BD�ϣ�HC��BD��HC���ӳ��߽���BAD��ƽ�����ڵ�E���Բ���CE��BD֮���������ϵ��˵�����ɣ�