题目内容
12.已知Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,求BC的长.分析 根据勾股定理求得AB的长度,然后利用射影定理来求得BH、BC的长度.
解答 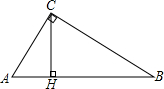 解:∵Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,
解:∵Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,
∴AH2=AC2-CH2=5.
∴AH=$\sqrt{5}$.
又∵CH2=AH•BH,
∴BH=$\frac{4}{\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,
∴BC2=BH•AB=$\frac{4\sqrt{5}}{5}$×($\sqrt{5}$+$\frac{4\sqrt{5}}{5}$)=$\frac{36}{5}$,则BC=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了射影定理:
①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.
②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
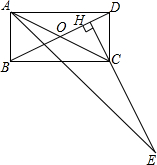 如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.
如图,在矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线交∠BAD的平分线于点E,试猜想CE与BD之间的数量关系,说明理由.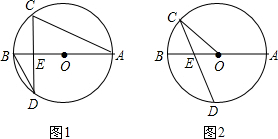
 已知:如图,E是BC上一点,AB=EC,AB∥CD,BC=CD.求证:AC=ED.
已知:如图,E是BC上一点,AB=EC,AB∥CD,BC=CD.求证:AC=ED. 在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.
在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.