题目内容
11.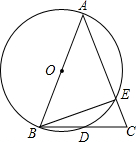 如图,已知△ABC中,AB=AC,∠A=45°,AB为⊙O的直径,AC交⊙O于点E,连接BE
如图,已知△ABC中,AB=AC,∠A=45°,AB为⊙O的直径,AC交⊙O于点E,连接BE(1)求∠EBC的度数;
(2)求证:BD=CD.
分析 (1)由AB为圆O的直径,利用直径所对的圆周角为直角得到∠AEB=90°,再由∠A=45°,利用直角三角形两锐角互余的性质得到∠ABE=45°,由AB=AC,由顶角的性质求出底角∠ABC的度数,由∠ABC-∠ABE即可求出∠EBC的度数.
(2)连接AD,由AB为圆O的直径,利用直径所对的圆周角为直角得到AD⊥BC,再根据等腰三角形三线合一的性质即可证得结论.
解答  解:∵AB为圆O的直径,
解:∵AB为圆O的直径,
∴∠AEB=90°,
∴∠ABE=90°-45°=45°,
∵AB=AC,
∴∠ABC=∠ACB=$\frac{180°-45°}{2}$=67.5°,
∴∠EBC=∠ABC-∠ABE=22.5°.
(2)连接AD,
∵AB是直径,
∴AD⊥BC,
∵AB=AC,
∴BD=DC.
点评 此题考查了圆周角定理,以及等腰三角形的性质,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
相关题目
13.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{3}{2}$ |
