题目内容
5.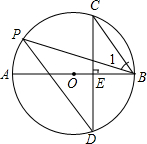 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.(1)求证:CB∥PD;
(2)若AB=10,sin∠P=$\frac{3}{5}$,求BC的长.
分析 (1)先根据圆周角定理得出∠P=∠C,再根据∠1=∠C可知∠1=∠P,由此可得出结论;
(2)连接AC,由AB是⊙O的直径,得到∠ACB=90°,得到∠BPD=∠CAB,于是得到$\frac{BC}{AB}$=$\frac{3}{5}$,根据已知条件即可得到结论.
解答 (1)证明:∵∠D=∠1,∠1=∠BCD,
∴∠D=∠BCD,
∴CB∥PD;
(2)解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠BPD=∠CAB,
∴sin∠CAB=sin∠BPD=$\frac{3}{5}$,
即$\frac{BC}{AB}$=$\frac{3}{5}$,
∵AB=10,
∴BC=6,即BC的长是6.
点评 本题考查的是圆周角定理,三角函数的定义,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
10.下列算式:①(-6)+(+3)=-9 ②-(-2)3=6 ③(+$\frac{6}{7}$)+(-$\frac{2}{7}$)=$\frac{4}{7}$ ④-5÷(-$\frac{1}{5}$)=25,其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知正六边形的半径为4,则这个正六边形的面积是( )
| A. | 4 | B. | 24 | C. | 4$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
8.某公司销售一种进价为20元/个的水杯,其销售量y(万个)与销售价格x(元/个)的变化如下表,销售过程中的其他开支(不含成本)总计40万元.
(1)求出该公司销售这种水杯的净利润z(万元)与销售价格x(元/个)的函数关系式,并求出销售价格定为多少时净利润最大?最大值是多少?
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
 如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.
如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.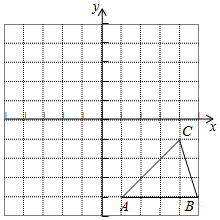 已知,方格纸中的每个小正方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
已知,方格纸中的每个小正方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).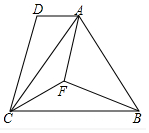 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB. 如图:F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图:F在BD上,BC、AD相交于点E,且AB∥CD∥EF,